
【題目】某水果種植基地引進一種新水果品種,經研究發現該水果每株的產量![]() (單位:
(單位:![]() )和與它“相近”的株數
)和與它“相近”的株數![]() 具有線性相關關系(兩株作物“相近”是指它們的直線距離不超過
具有線性相關關系(兩株作物“相近”是指它們的直線距離不超過![]() ),并分別記錄了相近株數為0,1,2,3,4時每株產量的相關數據如下:
),并分別記錄了相近株數為0,1,2,3,4時每株產量的相關數據如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出該種水果每株的產量![]() 關于它“相近”株數
關于它“相近”株數![]() 的回歸方程;
的回歸方程;
(2)有一種植戶準備種植該種水果500株,且每株與它“相近”的株數都為![]() ,計劃收獲后能全部售出,價格為10元
,計劃收獲后能全部售出,價格為10元![]() ,如果收入(收入=產量×價格)不低于25000元,則
,如果收入(收入=產量×價格)不低于25000元,則![]() 的最大值是多少?
的最大值是多少?
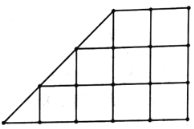
(3)該種植基地在如圖所示的直角梯形地塊的每個交叉點(直線的交點)處都種了一株該種水果,其中每個小正方形的邊長和直角三角形的直角邊長都為![]() ,已知該梯形地塊周邊無其他樹木影響,若從所種的該水果中隨機選取一株,試根據(1)中的回歸方程,預測它的產量的分布列與數學期望.
,已知該梯形地塊周邊無其他樹木影響,若從所種的該水果中隨機選取一株,試根據(1)中的回歸方程,預測它的產量的分布列與數學期望.
附:回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為: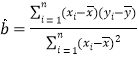 ,
,![]() .
.
 全能練考卷系列答案
全能練考卷系列答案 一課一練課時達標系列答案
一課一練課時達標系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線C:y2=2px(p>0)的焦點為F,拋物線C上橫坐標為3的點M到焦點F的距離為4.
(1)求拋物線C的方程;
(2)過拋物線C的焦點F且斜率為1的直線l交拋物線C于A、B兩點,求弦長|AB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于定義域為![]() 的函數
的函數![]() ,如果存在區間
,如果存在區間![]() ,其中
,其中![]() ,同時滿足:
,同時滿足:
①![]() 在
在![]() 內是單調函數:②當定義域為
內是單調函數:②當定義域為![]() 時,
時,![]() 的值域為
的值域為![]() ,則稱函數
,則稱函數![]() 是區間
是區間![]() 上的“保值函數”,區間
上的“保值函數”,區間![]() 稱為“保值函數”.
稱為“保值函數”.
(1)求證:函數![]() 不是定義域
不是定義域![]() 上的“保值函數”;
上的“保值函數”;
(2)若函數![]() (
(![]() )是區間
)是區間![]() 上的“保值函數”,求
上的“保值函數”,求![]() 的取值范圍;
的取值范圍;
(3)對(2)中函數![]() ,若不等式
,若不等式![]() 對
對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某水果種植基地引進一種新水果品種,經研究發現該水果每株的產量![]() (單位:
(單位:![]() )和與它“相近”的株數
)和與它“相近”的株數![]() 具有線性相關關系(兩株作物“相近”是指它們的直線距離不超過
具有線性相關關系(兩株作物“相近”是指它們的直線距離不超過![]() ),并分別記錄了相近株數為0,1,2,3,4時每株產量的相關數據如下:
),并分別記錄了相近株數為0,1,2,3,4時每株產量的相關數據如下:
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
(1)求出該種水果每株的產量![]() 關于它“相近”株數
關于它“相近”株數![]() 的回歸方程;
的回歸方程;
(2)該種植基地在如圖所示的長方形地塊的每個格點(橫縱直線的交點)處都種了一株該種水果,其中每個小正方形的面積都為![]() ,現從所種的該水果中隨機選取一株,試根據(1)中的回歸方程,預測它的產量的平均數.
,現從所種的該水果中隨機選取一株,試根據(1)中的回歸方程,預測它的產量的平均數.
附:回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為:
中斜率和截距的最小二乘法估計公式分別為: ,
,![]() .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,動圓
中,動圓![]() 與圓
與圓![]() 外切,與圓
外切,與圓![]() 內切.
內切.
(1)求動圓圓心![]() 的軌跡方程;
的軌跡方程;
(2)直線![]() 過點
過點![]() 且與動圓圓心
且與動圓圓心![]() 的軌跡交于
的軌跡交于![]() 、
、![]() 兩點.是否存在
兩點.是否存在![]() 面積的最大值,若存在,求出
面積的最大值,若存在,求出![]() 的面積;若不存在,說明理由.
的面積;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列四個命題:
①“若![]() ,則x,y互為倒數”的逆命題;
,則x,y互為倒數”的逆命題;
②“面積相等的三角形全等”的否命題;
③“若![]() ,則
,則![]() 有實根”的逆否命題;
有實根”的逆否命題;
④“若![]() ,則
,則![]() ”的逆命題。
”的逆命題。
其中真命題是( )
A.①②④B.②③④C.①②③D.①③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com