設a>0,已知函數f(x)=ex(ax2+x+1).
(Ⅰ)討論f(x)的單調性;
(Ⅱ)設g(x)=x2-2bx+4.若對?x1∈[0,1],?x2∈[1,2],使f(x1)≥g(x2).求實數b的取值范圍.
【答案】
分析:(I)先求出函數f(x)的導函數f'(x),然后討論a與0的大小關系,在函數的定義域內解不等式f'(x)>0和f'(x)<0,即可求出函數f(x)的單調區間;
(II)將f(x
1)≥g(x
2)問題轉化為求函數的最值問題:g(x)在[1,2]上的最小值不大于f(x)在[0,1]上的最小值1.
解答:解:(Ⅰ)∵f'(x)=e
x(ax
2+x+1+2ax+1)=e
x(x+2)(ax+1)(2分)
令f'(x)>0,得(x+2)(ax+1)>0,
∴
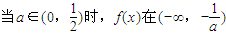
上遞增,在

上遞減,在-2,+∞上遞增;
當
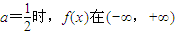
上遞增;
當
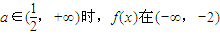
上遞增,在
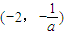
上遞減,在
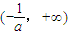
上遞增. (6分)
(Ⅱ)由(Ⅰ)知a>0時,f(x)在[0,1]總是單調增加,
故f(x)在[0,1]的最小值為f(0)=1. (8分)
由于“對?x
1∈[0,1],?x
2∈[1,2],使f(x
1)≥g(x
2)成立”等價于
“g(x)在[1,2]上的最小值不大于f(x)在[0,1]上的最小值1”. (9分)
又g(x)=(x-b)
2+4-b
2,x∈[1,2],所以,
①當b<1時,因為[g(x)]
min=g(1)=5-2b≤1,此時無解;
②當
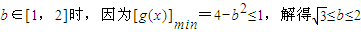
;
③當b∈(2,+∞)時,因為[g(x)]
min=g(2)=8-4b≤1,解得b>2;
綜上,b的取值范圍是

. (12分)
點評:本題主要考查了利用導數求閉區間上函數的最值,以及利用導數研究函數的單調性等基礎知識,考查綜合利用數學知識分析問題、解決問題的能力.

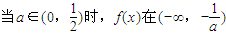 上遞增,在
上遞增,在 上遞減,在-2,+∞上遞增;
上遞減,在-2,+∞上遞增;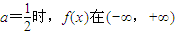 上遞增;
上遞增;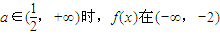 上遞增,在
上遞增,在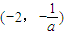 上遞減,在
上遞減,在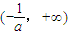 上遞增. (6分)
上遞增. (6分)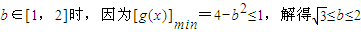 ;
; . (12分)
. (12分)
