


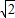 sin(x+
sin(x+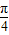 ),其最小正周期T=2π;
),其最小正周期T=2π;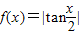 ,先去掉絕對值,利用正切的周期公式得到f(x)=tan
,先去掉絕對值,利用正切的周期公式得到f(x)=tan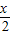 ,其最小正周期T=2π;
,其最小正周期T=2π;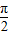
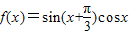 =(
=( sinx+
sinx+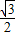 cosx)cosx=
cosx)cosx= sin2x+
sin2x+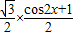
 sin2x+
sin2x+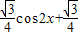 =
= sin(2x+
sin(2x+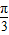 )+
)+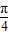 ,
,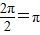
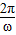 ,正切型最小正周期為T=
,正切型最小正周期為T=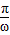 ,初次之外可以用圖象法,定義法,公倍數法,對于具體問題得具體分析.求三角函數的周期,要注意函數的三角變換,得到可以利用三角函數的周期公式來求解的形式,本題是一個中檔題目.
,初次之外可以用圖象法,定義法,公倍數法,對于具體問題得具體分析.求三角函數的周期,要注意函數的三角變換,得到可以利用三角函數的周期公式來求解的形式,本題是一個中檔題目. 

科目:高中數學 來源:2010-2011學年山東省濟南國語學校高一(下)期末數學試卷(解析版) 題型:選擇題
 上是增函數的是( )
上是增函數的是( )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com