
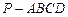 的底面
的底面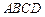 為菱形,
為菱形,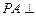 平面
平面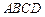 ,
,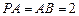 ,
,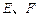 分別為
分別為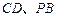 的中點,
的中點,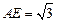 .
.
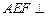 平面
平面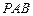 .
.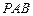 與平面
與平面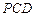 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.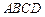 是菱形,
是菱形,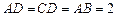 .
.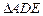 中
中 ,
,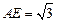 ,
,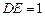 ,
,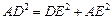 .
. ∴
∴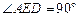 ,即
,即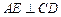 .
.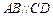 , ∴
, ∴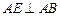 .…………………2分
.…………………2分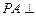 平面
平面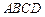 ,
, 平面
平面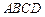 ,
,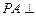
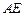 .又∵
.又∵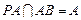 ,
,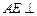 平面
平面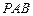 ,…………………………
,………………………… ……………4分
……………4分 平面
平面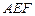 ,
,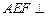 平面
平面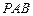 . ………………………………6分
. ………………………………6分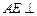 平面
平面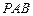 ,而
,而 平面
平面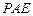 ,
,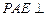 平面
平面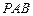 ………………………6分
………………………6分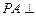 平面
平面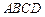 ,∴
,∴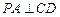 .
.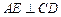 ,又
,又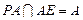
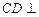 平面
平面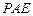 ,又
,又 平面
平面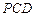 ,
,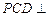 平面
平面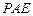 .…………………………8分
.…………………………8分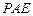 是平面
是平面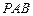
 與平面
與平面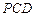 的公垂面.
的公垂面.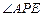 就是平面
就是平面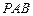 與平面
與平面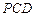 所成的銳二面角的平面角.……9分
所成的銳二面角的平面角.……9分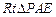 中,
中,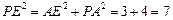 ,即
,即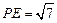 .……………10分
.……………10分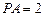 ,
, .
.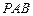 與平面
與平面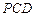 所成的銳二面角的余弦值為
所成的銳二面角的余弦值為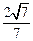 .…………12分
.…………12分 為原點,
為原點,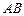 、
、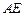 分別為
分別為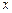 軸、
軸、 軸的正方向,
軸的正方向,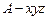 ,如圖.
,如圖.
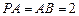 ,
,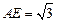 ,∴
,∴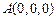 、
、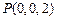 、
、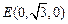 、
、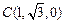 6分
6分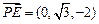 ,
,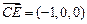 ,
,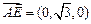 .………7分
.………7分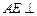 平面
平面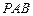 ,
,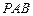 的一個法向量為
的一個法向量為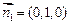 .……………………8分
.……………………8分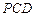 的一個法向量為
的一個法向量為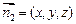 ,
,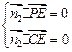 ,即
,即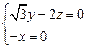 ,令
,令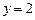 ,
,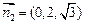 . …………………10分
. …………………10分 .
.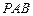 與平面
與平面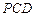 所成的銳二面角的余弦值為
所成的銳二面角的余弦值為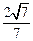 .……………12分
.……………12分

 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:不詳 題型:單選題
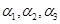 是三個相互平行的平面,平面
是三個相互平行的平面,平面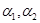 之間的距離為
之間的距離為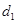 ,平面
,平面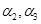 之間的距離為
之間的距離為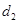 .直線
.直線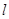 與
與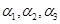 分別交于
分別交于 .那么
.那么 是
是 的 ( )
的 ( )| A.充分不必要條件 | B.必要不充分條件 |
| C.充分必要條件 | D.既不充分也不必要條件 |

查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
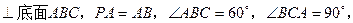
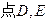 分別在棱
分別在棱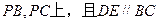 ,
,
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 中,底面
中,底面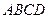 是矩形.已知
是矩形.已知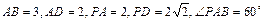 .
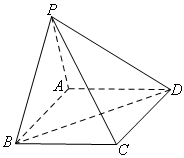
.
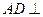 平面
平面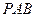 ;
;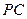 與
與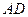 所成的角的大小;
所成的角的大小;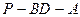 的大小.
的大小.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
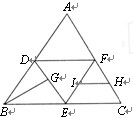
A.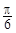 | B.a(chǎn)rccos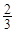 | C. | D.a(chǎn)rccos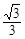 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
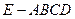 中,底面
中,底面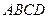 為正方形,
為正方形,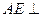 平面
平面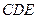 ,已知
,已知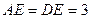 ,
,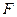 為線段
為線段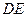 上的動點.
上的動點.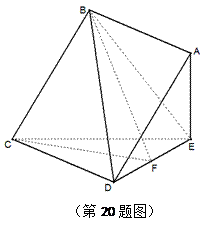
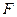 為
為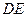 的中點,求證:
的中點,求證: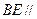 平面
平面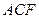 ;
;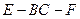 與二面角
與二面角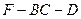 的大小相等,求
的大小相等,求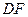 長.
長.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 12分)
12分)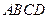 中,
中,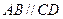
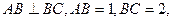
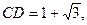 過
過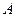 作
作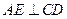 ,垂足為
,垂足為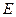 ,
,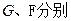
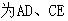 的中點,現(xiàn)將
的中點,現(xiàn)將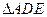 沿
沿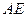 折疊,使得
折疊,使得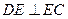 ,
,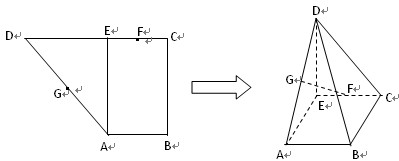
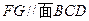 ;
; V,其外接球體積為
V,其外接球體積為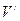 ,求V
,求V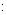
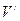 的值.
的值.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com