
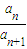 Tn為數(shù)列{cn}的前n項和,證明:Tn<
Tn為數(shù)列{cn}的前n項和,證明:Tn<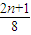 .
. =4(an-1-
=4(an-1- );即{an-
);即{an- }為等比數(shù)列,可求數(shù)列{an}的通項公式;
}為等比數(shù)列,可求數(shù)列{an}的通項公式; =4(an-1-
=4(an-1- );⇒{an-
);⇒{an- }是以a1-
}是以a1- 為首項4為公比的等比數(shù)列.
為首項4為公比的等比數(shù)列. =
=
 =
= •4n-1⇒an=
•4n-1⇒an= +
+ •4n-1=
•4n-1= .
. =
=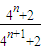 <
<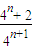 =
= +
+
 =
= <
<
 +
+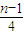 +2(
+2(
 +…+
+…+ )
) +
+ +2×
+2× =
= -
- <
<
 .
.

 課課優(yōu)能力培優(yōu)100分系列答案
課課優(yōu)能力培優(yōu)100分系列答案 優(yōu)百分課時互動系列答案
優(yōu)百分課時互動系列答案科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| A、16 | B、8 | C、4 | D、不確定 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com