
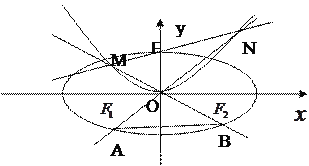
【題目】如圖,橢圓![]()
![]() 的左右焦點分別為的
的左右焦點分別為的![]() 、
、![]() ,離心率為
,離心率為![]() ;過拋物線
;過拋物線![]() 焦點
焦點![]() 的直線交拋物線于
的直線交拋物線于![]() 、
、![]() 兩點,當
兩點,當![]() 時,
時, ![]() 點在
點在![]() 軸上的射影為
軸上的射影為![]() 。連結
。連結![]() 并延長分別交
并延長分別交![]() 于
于![]() 、
、![]() 兩點,連接
兩點,連接![]() ;
; ![]() 與
與![]() 的面積分別記為
的面積分別記為![]() ,
, ![]() ,設
,設![]() .
.
(Ⅰ)求橢圓![]() 和拋物線
和拋物線![]() 的方程;
的方程;
(Ⅱ)求![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ,
,![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(Ⅰ )由題意得得![]() ,根據點M在拋物線上得
,根據點M在拋物線上得![]() ,又由
,又由![]() ,得
,得 ![]() ,可得
,可得![]() ,解得
,解得![]() ,從而得
,從而得![]() ,可得曲線方程。(Ⅱ )設
,可得曲線方程。(Ⅱ )設![]() ,
, ![]() ,分析可得
,分析可得![]() ,先設出直線
,先設出直線![]() 的方程為
的方程為![]()
![]() ,由
,由![]() ,解得
,解得![]() ,從而可求得
,從而可求得![]() ,同理可得
,同理可得![]() ,故可將
,故可將![]() 化為m的代數式,用基本不等式求解可得結果。
化為m的代數式,用基本不等式求解可得結果。
試題解析:
(Ⅰ)由拋物線定義可得![]() ,
,
∵點M在拋物線![]() 上,
上,
∴![]() ,即
,即![]() ①
①
又由![]() ,得
,得 ![]()
將上式代入①,得![]()
解得![]()
∴![]()
![]() ,
,
所以曲線![]() 的方程為
的方程為![]() ,曲線
,曲線![]() 的方程為
的方程為![]() 。
。
(Ⅱ)設直線![]() 的方程為
的方程為![]() ,
,
由![]() 消去y整理得
消去y整理得![]() ,
,
設![]() ,
, ![]() .
.
則![]() ,
,
設![]() ,
, ![]() ,
,
則![]() ,
,
所以![]() , ②
, ②
設直線![]() 的方程為
的方程為![]()
![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() ,
,
由②可知,用![]() 代替
代替![]() ,
,
可得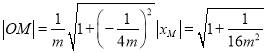 ,
,
由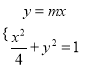 ,解得
,解得![]() ,
,
所以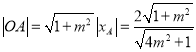 ,
,
用![]() 代替
代替![]() ,可得
,可得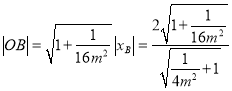
所以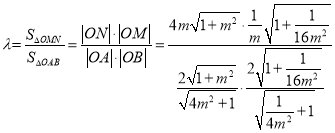
![]()
![]() ,當且僅當
,當且僅當![]() 時等號成立。
時等號成立。
所以![]() 的取值范圍為
的取值范圍為![]() .
.


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,四棱錐O﹣ABCD的底面是邊長為1的菱形,OA=2,∠ABC=60°,OA⊥平面ABCD,M、N分別是OA、BC的中點.
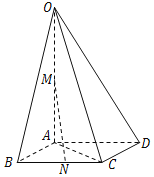
(1)求證:直線MN∥平面OCD;
(2)求點M到平面OCD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過橢圓
,過橢圓![]() 的焦點且垂直于
的焦點且垂直于![]() 軸的直線被橢圓
軸的直線被橢圓![]() 截得的弦長為
截得的弦長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設點![]() 均在橢圓
均在橢圓![]() 上,點
上,點![]() 在拋物線
在拋物線![]() 上,若
上,若![]() 的重心為坐標原點
的重心為坐標原點![]() ,且
,且![]() 的面積為
的面積為![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,直線l的極坐標方程為ρcosθ=4,曲線C的極坐標方程為ρ=2cosθ+2sinθ,以極點為坐標原點O,極軸為x軸的正半軸建立直角坐標系,射線l':y=kx(x≥0,0<k<1)與曲線C交于O,M兩點.
(Ⅰ)寫出直線l的直角坐標方程以及曲線C的參數方程;
(Ⅱ)若射線l′與直線l交于點N,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司![]() 人數眾多
人數眾多![]() 為鼓勵員工利用網絡進行營銷,準備為員工辦理手機流量套餐.為了解員工手機流量使用情況,按照男員工和女員工
為鼓勵員工利用網絡進行營銷,準備為員工辦理手機流量套餐.為了解員工手機流量使用情況,按照男員工和女員工![]() 的比例分層抽樣,得到
的比例分層抽樣,得到![]() 名員工的月使用流量
名員工的月使用流量![]() (單位:
(單位:![]() )的數據,其頻率分布直方圖如圖所示.
)的數據,其頻率分布直方圖如圖所示.
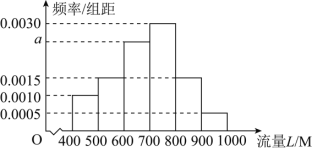
(1)求![]() 的值,并估計這
的值,并估計這![]() 名員工月使用流量的平均值
名員工月使用流量的平均值![]() (同一組中的數據用中點值代表
(同一組中的數據用中點值代表![]() ;
;
(2)若將月使用流量在![]() 以上(含
以上(含![]() )的員工稱為“手機營銷達人”,填寫下面的
)的員工稱為“手機營銷達人”,填寫下面的![]() 列聯表,能否有超過
列聯表,能否有超過![]() 的把握認為“成為手機營銷達人與員工的性別有關”;
的把握認為“成為手機營銷達人與員工的性別有關”;
男員工 | 女員工 | 合計 | |
手機營銷達人 | 5 | ||
非手機營銷達人 | |||
合計 | 200/span> |
參考公式及數據:![]() ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(3)若這![]() 名員工中有
名員工中有![]() 名男員工每月使用流量在
名男員工每月使用流量在![]() ,從每月使用流量在
,從每月使用流量在![]() 的員工中隨機抽取名
的員工中隨機抽取名![]() 進行問卷調查,記女員工的人數為
進行問卷調查,記女員工的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《高中數學課程標準》(2017版)規定了數學直觀想象學科的六大核心素養,為了比較甲、乙兩名高二學生的數學核心素養水平,現以六大素養為指標對二人進行了測驗,根據測驗結果繪制了雷達圖(如圖,每項指標值滿分為5分,分值高者為優),則下面敘述正確的是(注:雷達圖![]() ,又可稱為戴布拉圖、蜘蛛網圖
,又可稱為戴布拉圖、蜘蛛網圖![]() ,可用于對研究對象的多維分析)( )
,可用于對研究對象的多維分析)( )
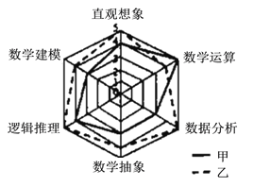
A.甲的直觀想象素養高于乙
B.甲的數學建模素養優于數據分析素養
C.乙的數學建模素養與數學運算素養一樣
D.乙的六大素養整體水平低于甲
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】BMI指數(身體質量指數,英文為BodyMassIndex,簡稱BMI)是衡量人體胖瘦程度的一個標準,BMI=體重(kg)/身高(m)的平方.根據中國肥胖問題工作組標準,當BMI≥28時為肥胖.某地區隨機調查了1200名35歲以上成人的身體健康狀況,其中有200名高血壓患者,被調查者的頻率分布直方圖如下:
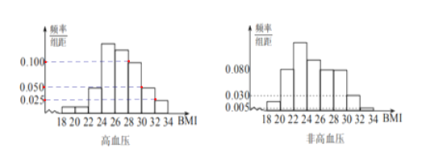
(1)求被調查者中肥胖人群的BMI平均值![]() ;
;
(2)填寫下面列聯表,并判斷是否有99.9%的把握認為35歲以上成人患高血壓與肥胖有關.
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
肥胖 | 不肥胖 | 合計 | |
高血壓 | |||
非高血壓 | |||
合計 |
附: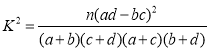 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為1,線段
的棱長為1,線段![]() 上有兩個動點
上有兩個動點![]() ,且
,且![]() ,現有如下四個結論:
,現有如下四個結論:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱錐
三棱錐![]() 的體積為定值;
的體積為定值;![]() 異面直線
異面直線![]() 所成的角為定值,
所成的角為定值,
其中正確結論的序號是______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com