Question

關于x的方程x³-3x²-a=0有3個不同的實數解，則a的取值范圍是    ．

Answer 1

【答案】分析：關于x的方程x³-3x²-a=0有3個不同的實數解?函數y=x³-3x²與y=a由三個不同的交點，利用導數先得出函數y=f（x）的單調性并畫出圖象，進而即可得出答案．
解答：解：由x³-3x²-a=0，得x³-3x²=a．
令f（x）=x³-3x²，解x³-3x²=0，得x₁=x₂=0，或x₃=3，即函數f（x）有一個零點3，和一個二重零點0．
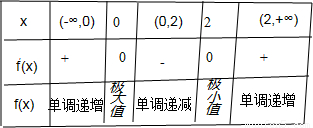
又f^′（x）=3x²-6x=3x（x-2），令f^′（x）=0，則x=0或2．列表如下：
由表格可以看出：
函數f（x）在區間（-∞，0）上單調遞增，在區間（0，2）上單調遞減，在區間（2，+∞）上單調遞增．
在x=0時取得極大值，且f（0）=0；在x=2時取得極小值，且f（2）=-4．
綜上可畫出函數y=f（x）的圖象，如下圖：
要使函數y=f（x）與y=a由三個不同的交點，則必須滿足-4＜x＜0．
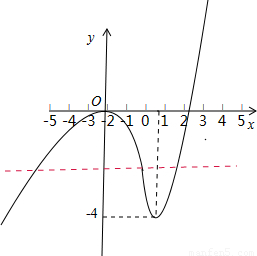
此時滿足 關于x的方程x³-3x²-a=0有3個不同的實數解．
故答案為（-4，0）．
點評：把方程的解得問題轉化問題函數的交點問題和熟練應用導數得到函數的單調性并畫出圖象是解題的關鍵．