
【題目】已知單調(diào)遞增的等比數(shù)列![]() 滿足:
滿足:![]() .且
.且![]() 是
是![]() ,
,![]() 的等差中項.又數(shù)列
的等差中項.又數(shù)列![]() 滿足:
滿足:![]() ,
,![]() ,
,![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)若![]() ,且數(shù)列
,且數(shù)列![]() 為等比數(shù)列,求
為等比數(shù)列,求![]() 的值;
的值;
(3)若![]() ,且
,且![]() 為數(shù)列
為數(shù)列![]() 的最小項,求
的最小項,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)根據(jù)等比數(shù)列以及等差數(shù)列的性質(zhì)求出數(shù)列的通項公式即可;
(2)代入![]() 的值,設(shè)出數(shù)列
的值,設(shè)出數(shù)列![]() 的公比,得到關(guān)于公比和和
的公比,得到關(guān)于公比和和![]() 的方程組,解出即可;
的方程組,解出即可;
(3)求出數(shù)列![]() 的通項公式,結(jié)合函數(shù)的單調(diào)性以及
的通項公式,結(jié)合函數(shù)的單調(diào)性以及![]() 為數(shù)列
為數(shù)列![]() 的最小項,得到關(guān)于
的最小項,得到關(guān)于![]() 的不等式組,解出即可.
的不等式組,解出即可.
(1)設(shè)等比數(shù)列![]() 的公比為
的公比為![]() ,
,
因為![]() .且
.且![]() 是
是![]() ,
,![]() 的等差中項,
的等差中項,
所以![]() ,
,
即![]() .
.
解得![]() ,
,![]() 或
或![]() (舍去).
(舍去).
所以![]() .
.
(2)![]() 時,
時,![]() ,
,
而![]() ,
,
所以![]() ,
,
而數(shù)列![]() 是等比數(shù)列,設(shè)公比是
是等比數(shù)列,設(shè)公比是![]() ,
,
則 ,
,
解得![]() 或
或![]() .
.
所以![]() 或
或![]() .
.
(3)若![]() ,
,
故![]() ,
,
![]()
令![]() ,其中
,其中![]() ,
,
若![]() 為數(shù)列
為數(shù)列![]() 的最小項,而
的最小項,而![]() 是遞增數(shù)列,
是遞增數(shù)列,
則![]() 是遞減數(shù)列,故
是遞減數(shù)列,故![]() ,
,
故只需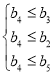 ,即
,即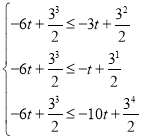 ,解得
,解得![]() .
.


 各地期末復(fù)習(xí)特訓(xùn)卷系列答案
各地期末復(fù)習(xí)特訓(xùn)卷系列答案 小博士期末闖關(guān)100分系列答案
小博士期末闖關(guān)100分系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某調(diào)查機構(gòu)對全國互聯(lián)網(wǎng)行業(yè)進行調(diào)查統(tǒng)計,得到整個互聯(lián)網(wǎng)行業(yè)從業(yè)者年齡分布餅狀圖,90后從事互聯(lián)網(wǎng)行業(yè)崗位分布條形圖,則下列結(jié)論中不正確的是( )
注:90后指1990年及以后出生,80后指1980-1989年之間出生,80前指1979年及以前出生.


A.互聯(lián)網(wǎng)行業(yè)從業(yè)人員中90后占一半以上
B.互聯(lián)網(wǎng)行業(yè)中從事技術(shù)崗位的人數(shù)超過總?cè)藬?shù)的![]()
C.互聯(lián)網(wǎng)行業(yè)中從事運營崗位的人數(shù)90后比80前多
D.互聯(lián)網(wǎng)行業(yè)中從事技術(shù)崗位的人數(shù)90后比80后多
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列四個命題中,真命題的個數(shù)是 ( )
①命題:“已知![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要條件”;
”的充分不必要條件”;
②命題:“p且q為真”是“p或q為真”的必要不充分條件;
③命題:已知冪函數(shù)![]() 的圖象經(jīng)過點(2,
的圖象經(jīng)過點(2,![]() ),則f(4)的值等于
),則f(4)的值等于![]() ;
;
④命題:若![]() ,則
,則![]() .
.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的短軸長為
的短軸長為![]() ,過點
,過點![]() ,
,![]() 的直線傾斜角為
的直線傾斜角為![]() .
.
(1)求橢圓的方程;
(2)是否存在過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() ,使直線
,使直線![]() 交橢圓于
交橢圓于![]() 兩點,以
兩點,以![]() 為直徑的圓過點
為直徑的圓過點![]() ?若存在,求出直線
?若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
,![]() ,其中
,其中![]() ,
,![]() 為正實數(shù).
為正實數(shù).
(1)若![]() 的圖象總在函數(shù)
的圖象總在函數(shù)![]() 的圖象的下方,求實數(shù)
的圖象的下方,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)設(shè)![]() ,證明:對任意
,證明:對任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() .
.
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() 存在兩個零點
存在兩個零點![]() .
.
①實數(shù)![]() 的取值范圍;
的取值范圍;
②證明:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,過點
,過點![]() 的直線
的直線![]() 與
與![]() 有兩個不同的交點
有兩個不同的交點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,
,![]() 為坐標原點,直線
為坐標原點,直線![]() 與直線
與直線![]() 分別交直線
分別交直線![]() 于點
于點![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)求線段![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知動圓![]() 與圓
與圓![]() :
:![]() 外切且與
外切且與![]() 軸相切.
軸相切.
(1)求圓心![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 交曲線
交曲線![]() 于
于![]() ,
,![]() 兩點,
兩點,
①若![]() ,求直線
,求直線![]() 的方程;
的方程;
②過![]() ,
,![]() 兩點分別作曲線
兩點分別作曲線![]() 的切線
的切線![]() ,
,![]() ,求證:
,求證:![]() ,
,![]() 的交點恒在一條定直線上.
的交點恒在一條定直線上.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在全面抗擊新冠肺炎疫情這一特殊時期,我市教育局提出“停課不停學(xué)”的口號,鼓勵學(xué)生線上學(xué)習(xí).某校數(shù)學(xué)教師為了調(diào)查高三學(xué)生數(shù)學(xué)成績與線上學(xué)習(xí)時間之間的相關(guān)關(guān)系,對高三年級隨機選取45名學(xué)生進行跟蹤問卷,其中每周線上學(xué)習(xí)數(shù)學(xué)時間不少于5小時的有19人,余下的人中,在檢測考試中數(shù)學(xué)平均成績不足120分的占![]() ,統(tǒng)計成績后得到如下
,統(tǒng)計成績后得到如下![]() 列聯(lián)表:
列聯(lián)表:
分數(shù)不少于120分 | 分數(shù)不足120分 | 合計 | |
線上學(xué)習(xí)時間不少于5小時 | 4 | 19 | |
線上學(xué)習(xí)時間不足5小時 | |||
合計 | 45 |
(1)請完成上面![]() 列聯(lián)表;并判斷是否有99%的把握認為“高三學(xué)生的數(shù)學(xué)成績與學(xué)生線上學(xué)習(xí)時間有關(guān)”;
列聯(lián)表;并判斷是否有99%的把握認為“高三學(xué)生的數(shù)學(xué)成績與學(xué)生線上學(xué)習(xí)時間有關(guān)”;
(2)①按照分層抽樣的方法,在上述樣本中從分數(shù)不少于120分和分數(shù)不足120分的兩組學(xué)生中抽取9名學(xué)生,設(shè)抽到不足120分且每周線上學(xué)習(xí)時間不足5小時的人數(shù)是![]() ,求
,求![]() 的分布列(概率用組合數(shù)算式表示);
的分布列(概率用組合數(shù)算式表示);
②若將頻率視為概率,從全校高三該次檢測數(shù)學(xué)成績不少于120分的學(xué)生中隨機抽取20人,求這些人中每周線上學(xué)習(xí)時間不少于5小時的人數(shù)的期望和方差.
(下面的臨界值表供參考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式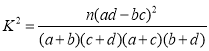 其中
其中![]() )
)
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com