
【題目】為了解學生寒假期間學習情況,學校對某班男、女學生學習時間進行調查,學習時間按整小時統計,調查結果繪成折線圖如下:

(1)已知該校有![]() 名學生,試估計全校學生中,每天學習不足
名學生,試估計全校學生中,每天學習不足![]() 小時的人數.
小時的人數.
(2)若從學習時間不少于![]() 小時的學生中選取
小時的學生中選取![]() 人,設選到的男生人數為
人,設選到的男生人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列.
的分布列.
(3)試比較男生學習時間的方差![]() 與女生學習時間方差
與女生學習時間方差![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
【答案】(1)240人(2)見解析(3)![]()
【解析】試題分析:(1)根據題意,由折線圖分析可得20名學生中有12名學生每天學習不足4小時,進而可以估計校400名學生中天學習不足4小時的人數;
(2)學習時間不少于4本的學生共8人,其中男學生人數為4人,故X的取值為0,1,2,3,4;由古典概型公式計算可得X=0,1,2,3,4的概率,進而可得隨機變量X的分布列;
(3)根據題意,分析折線圖,求出男生、女生的學習時間方差,比較可得答案.
試題解析:
(1)由折線圖可得共抽取了![]() 人,其中男生中學習時間不足
人,其中男生中學習時間不足![]() 小時的有
小時的有![]() 人,女生中學習時間不足
人,女生中學習時間不足![]() 小時的有
小時的有![]() 人.
人.
∴可估計全校中每天學習不足![]() 小時的人數為:
小時的人數為: ![]() 人.
人.
(2)學習時間不少于![]() 本的學生共
本的學生共![]() 人,其中男學生人數為
人,其中男學生人數為![]() 人,故
人,故![]() 的所有可能取值為
的所有可能取值為![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
由題意可得![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
所以隨機變量![]() 的分布列為
的分布列為
|
|
|
|
|
|
|
|
|
|
|
|
∴均值![]()
![]()
![]() .
.
(3)由折線圖可得![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖所示,在三棱臺![]() 中,點
中,點![]() 在
在![]() 上,且
上,且![]() ,點
,點![]() 是
是![]() 內(含邊界)的一個動點,且有平面
內(含邊界)的一個動點,且有平面![]() 平面
平面![]() ,則動點
,則動點![]() 的軌跡是( )
的軌跡是( )

A. 平面B. 直線C. 線段,但只含1個端點D. 圓
查看答案和解析>>
科目:高中數學 來源: 題型:
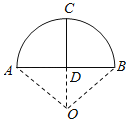
【題目】《九章算術》是我國古代數學成就的杰出代表作,其中《方田》章給出計算弧田面積所用的經驗方式為:弧田面積=![]() (弦×矢+矢2),弧田(如圖)由圓弧和其所對弦所圍成,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差,現有圓心角為
(弦×矢+矢2),弧田(如圖)由圓弧和其所對弦所圍成,公式中“弦”指圓弧所對弦長,“矢”等于半徑長與圓心到弦的距離之差,現有圓心角為![]() ,半徑等于
,半徑等于![]() 米的弧田,按照上述經驗公式計算所得弧田面積約是
米的弧田,按照上述經驗公式計算所得弧田面積約是 ![]()
A. ![]() 平方米 B.
平方米 B. ![]() 平方米
平方米
C. ![]() 平方米 D.
平方米 D. ![]() 平方米
平方米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-5:不等式選講】
已知函數f(x)=|x+1|+|x-3|.
(1)若關于x的不等式f(x)<a有解,求實數a的取值范圍:
(2)若關于x的不等式f(x)<a的解集為(b, ![]() ),求a+b的值.
),求a+b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著網絡的發展,網上購物越來越受到人們的喜愛,各大購物網站為增加收入,促銷策略越來越多樣化,促銷費用也不斷增加,下表是某購物網站![]() 年
年![]() 月促銷費用
月促銷費用![]() (萬元)和產品銷量
(萬元)和產品銷量![]() (萬件)的具體數據.
(萬件)的具體數據.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促銷費用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
產品銷量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根據數據可知![]() 與
與![]() 具有線性相關關系,請建立
具有線性相關關系,請建立![]() 關于
關于![]() 的回歸方程
的回歸方程![]() (系數精確到
(系數精確到![]() );
);
(2)已知![]() 月份該購物網站為慶祝成立
月份該購物網站為慶祝成立![]() 周年,特定制獎勵制度:用
周年,特定制獎勵制度:用![]() (單位:件)表示日銷量,若
(單位:件)表示日銷量,若![]() ,則每位員工每日獎勵
,則每位員工每日獎勵![]() 元;若
元;若![]() ,每位員工每日獎勵
,每位員工每日獎勵![]() 元;若
元;若![]() ,則每位員工每日獎勵
,則每位員工每日獎勵![]() 元.現已知該網站
元.現已知該網站![]() 月份日銷量
月份日銷量![]() 服從正態分布
服從正態分布![]() ,請你計算某位員工當月獎勵金額總數大約為多少元.(當月獎勵金額總數精確到百分位)
,請你計算某位員工當月獎勵金額總數大約為多少元.(當月獎勵金額總數精確到百分位)
參考數據:![]() ,
,![]() ,其中
,其中![]() 分別為第
分別為第![]() 個月的促銷費用和產品銷量,
個月的促銷費用和產品銷量,![]() .
.
參考公式:①對于一組數據![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 ,
,![]() .
.
②若隨機變量![]() 服從正態分布
服從正態分布![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面六個命題中,其中正確的命題序號為______________.
①函數![]() 的最小正周期為
的最小正周期為![]() ;
;
②函數![]() 的圖象關于點
的圖象關于點![]() 對稱;
對稱;
③函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱;
對稱;
④函數![]() ,
,![]() 的單調遞減區間為
的單調遞減區間為![]() ;
;
⑤將函數![]() 向右平移
向右平移![]() (
(![]() )個單位所得圖象關于
)個單位所得圖象關于![]() 軸對稱,則
軸對稱,則![]() 的最小正值為
的最小正值為![]() ;
;
⑥關于![]() 的方程
的方程![]() 的兩個實根中,一個根比1大,一個根比-1小,則
的兩個實根中,一個根比1大,一個根比-1小,則![]() 的取值范圍為
的取值范圍為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】分形幾何學是美籍法國數學家伯努瓦.![]() .曼德爾布羅特在20世紀70年代創立的一門新學科,它的創立,為解決傳統科學眾多領域的難題提供了全新的思路,如圖是按照一定的分形規律生產成一個數形圖,則第13行的實心圓點的個數是______.
.曼德爾布羅特在20世紀70年代創立的一門新學科,它的創立,為解決傳統科學眾多領域的難題提供了全新的思路,如圖是按照一定的分形規律生產成一個數形圖,則第13行的實心圓點的個數是______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】美國對中國芯片的技術封鎖激發了中國“芯”的研究熱潮.某公司研發的![]() ,
,![]() 兩種芯片都已經獲得成功.該公司研發芯片已經耗費資金
兩種芯片都已經獲得成功.該公司研發芯片已經耗費資金![]() 千萬元,現在準備投入資金進行生產.經市場調查與預測,生產
千萬元,現在準備投入資金進行生產.經市場調查與預測,生產![]() 芯片的毛收入與投入的資金成正比,已知每投入
芯片的毛收入與投入的資金成正比,已知每投入![]() 千萬元,公司獲得毛收入
千萬元,公司獲得毛收入![]() 千萬元;生產
千萬元;生產![]() 芯片的毛收入
芯片的毛收入![]() (千萬元)與投入的資金
(千萬元)與投入的資金![]() (千萬元)的函數關系為
(千萬元)的函數關系為![]() ,其圖像如圖所示.
,其圖像如圖所示.

(1)試分別求出生產![]() ,
,![]() 兩種芯片的毛收入
兩種芯片的毛收入![]() (千萬元)與投入資金
(千萬元)與投入資金![]() (千萬元)的函數關系式;
(千萬元)的函數關系式;
(2)現在公司準備投入![]() 億元資金同時生產
億元資金同時生產![]() ,
,![]() 兩種芯片,求可以獲得的最大利潤是多少.
兩種芯片,求可以獲得的最大利潤是多少.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com