
【題目】交強(qiáng)險(xiǎn)是車(chē)主必須為機(jī)動(dòng)車(chē)購(gòu)買(mǎi)的險(xiǎn)種,若普通6座以下私家車(chē)投保交強(qiáng)險(xiǎn)第一年的費(fèi)用(基準(zhǔn)保費(fèi))統(tǒng)一為![]() 元,在下一年續(xù)保時(shí),實(shí)行的是費(fèi)率浮動(dòng)機(jī)制,保費(fèi)與上一年度車(chē)輛發(fā)生道路交通事故的情況相聯(lián)系,發(fā)生交通事故的次數(shù)越多,費(fèi)率也就越高,具體浮動(dòng)情況如下表:
元,在下一年續(xù)保時(shí),實(shí)行的是費(fèi)率浮動(dòng)機(jī)制,保費(fèi)與上一年度車(chē)輛發(fā)生道路交通事故的情況相聯(lián)系,發(fā)生交通事故的次數(shù)越多,費(fèi)率也就越高,具體浮動(dòng)情況如下表:
交強(qiáng)險(xiǎn)浮動(dòng)因素和浮動(dòng)費(fèi)率比率表 | ||
浮動(dòng)因素 | 浮動(dòng)比率 | |
| 上一個(gè)年度未發(fā)生有責(zé)任道路交通事故 | 下浮10% |
| 上兩個(gè)年度未發(fā)生責(zé)任道路交通事故 | 下浮20% |
| 上三個(gè)及以上年度未發(fā)生有責(zé)任道路交通事故 | 下浮30% |
| 上一個(gè)年度發(fā)生一次有責(zé)任不涉及死亡的道路交通事故 | 0% |
| 上一個(gè)年度發(fā)生兩次及兩次以上有責(zé)任道路交通事故 | 上浮10% |
| 上一個(gè)年度發(fā)生有責(zé)任道路交通死亡事故 | 上浮30% |
某機(jī)購(gòu)為了研究某一品牌普通6座以下私家車(chē)的投保情況,隨機(jī)抽取了60輛車(chē)齡已滿三年的該品牌同型號(hào)私家車(chē)的下一年續(xù)保時(shí)的情況,統(tǒng)計(jì)得到了下面的表格:
類(lèi)型 |
|
|
|
|
|
|
數(shù)量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一輛普通6座以下私家車(chē)在第四年續(xù)保時(shí)保費(fèi)高于基本保費(fèi)的頻率;
(2)某二手車(chē)銷(xiāo)售商專(zhuān)門(mén)銷(xiāo)售這一品牌的二手車(chē),且將下一年的交強(qiáng)險(xiǎn)保費(fèi)高于基本保費(fèi)的車(chē)輛記為事故車(chē),假設(shè)購(gòu)進(jìn)一輛事故車(chē)虧損5000元,一輛非事用戶車(chē)盈利10000元,且各種投保類(lèi)型車(chē)的頻率與上述機(jī)構(gòu)調(diào)查的頻率一致,完成下列問(wèn)題:
①若該銷(xiāo)售商店內(nèi)有六輛(車(chē)齡已滿三年)該品牌二手車(chē),某顧客欲在店內(nèi)隨機(jī)挑選兩輛車(chē),求這兩輛車(chē)恰好有一輛為事故車(chē)的概率;
②若該銷(xiāo)售商一次購(gòu)進(jìn)120輛(車(chē)齡已滿三年)該品牌二手車(chē),求一輛車(chē)盈利的平均值.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 元.
元.
【解析】試題分析:(1)利用等可能事件概率計(jì)算公式,能求出一輛普通6座以下私家車(chē)第四年續(xù)保時(shí)保費(fèi)高于基本保費(fèi)的概率;(2)①由統(tǒng)計(jì)數(shù)據(jù)可知,該銷(xiāo)售商店內(nèi)的六輛該品牌車(chē)齡已滿三年的二手車(chē)有兩輛事故車(chē),設(shè)為![]() ,四輛非事故車(chē)設(shè)為
,四輛非事故車(chē)設(shè)為![]() ,利用列舉法求出從六輛車(chē)中隨機(jī)挑選兩輛車(chē)的基本事件總和其中兩輛車(chē)恰好有一輛事故車(chē)包含的基本事件個(gè)數(shù),由此能求出該顧客在店內(nèi)隨機(jī)挑選的兩輛車(chē)恰好有一輛事故車(chē)的概率;②由統(tǒng)計(jì)數(shù)據(jù)可知,該銷(xiāo)售商一次購(gòu)進(jìn)120輛該品牌車(chē)齡已滿三年的二手車(chē)有事故車(chē)
,利用列舉法求出從六輛車(chē)中隨機(jī)挑選兩輛車(chē)的基本事件總和其中兩輛車(chē)恰好有一輛事故車(chē)包含的基本事件個(gè)數(shù),由此能求出該顧客在店內(nèi)隨機(jī)挑選的兩輛車(chē)恰好有一輛事故車(chē)的概率;②由統(tǒng)計(jì)數(shù)據(jù)可知,該銷(xiāo)售商一次購(gòu)進(jìn)120輛該品牌車(chē)齡已滿三年的二手車(chē)有事故車(chē)![]() 輛,非事故車(chē)
輛,非事故車(chē)![]() 輛,由此能求出一輛車(chē)盈利的平均值.
輛,由此能求出一輛車(chē)盈利的平均值.
試題解析:(1)一輛普通6座以下私家車(chē)第四年續(xù)保時(shí)保費(fèi)高于基本保費(fèi)的頻率為![]() .
.
(2)①由統(tǒng)計(jì)數(shù)據(jù)可知,該銷(xiāo)售商店內(nèi)的六輛該品牌車(chē)齡已滿三年的二手車(chē)有兩輛事故車(chē),設(shè)為![]() ,四輛非事故車(chē)設(shè)為
,四輛非事故車(chē)設(shè)為![]() ,從六輛車(chē)中隨機(jī)挑選兩輛車(chē)共有:
,從六輛車(chē)中隨機(jī)挑選兩輛車(chē)共有:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 總共15種情況.
總共15種情況.
其中兩輛車(chē)恰好有一輛事故車(chē)共有:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,總共8種情況.
,總共8種情況.
所以該顧客在店內(nèi)隨機(jī)挑選的兩輛車(chē)恰好有一輛事故車(chē)的概率為![]() .
.
②由統(tǒng)計(jì)數(shù)據(jù)可知,該銷(xiāo)售商一次購(gòu)進(jìn)120輛該品牌車(chē)齡已滿三年的二手車(chē)有事故車(chē)40輛,非事故車(chē)80輛,
所以一輛車(chē)盈利的平均值為![]() 元.
元.


 名師導(dǎo)航單元期末沖刺100分系列答案
名師導(dǎo)航單元期末沖刺100分系列答案 名校名卷單元同步訓(xùn)練測(cè)試題系列答案
名校名卷單元同步訓(xùn)練測(cè)試題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知數(shù)列![]() 的前n項(xiàng)的和Sn,點(diǎn)(n,Sn)在函數(shù)
的前n項(xiàng)的和Sn,點(diǎn)(n,Sn)在函數(shù)![]() =2x2+4x圖象上:
=2x2+4x圖象上:
(1)證明![]() 是等差數(shù)列;
是等差數(shù)列;
(2)若函數(shù)![]() ,數(shù)列{bn}滿足bn=
,數(shù)列{bn}滿足bn=![]() ,記cn=anbn,求數(shù)列
,記cn=anbn,求數(shù)列![]() 前n項(xiàng)和Tn;
前n項(xiàng)和Tn;
(3)是否存在實(shí)數(shù)λ,使得當(dāng)x≤λ時(shí),f(x)=﹣x2+4x﹣![]() ≤0對(duì)任意n∈N*恒成立?若存在,求出最大的實(shí)數(shù)λ,若不存在,說(shuō)明理由.
≤0對(duì)任意n∈N*恒成立?若存在,求出最大的實(shí)數(shù)λ,若不存在,說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程.
在平面直角坐標(biāo)系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),以
為參數(shù)).以坐標(biāo)原點(diǎn)為極點(diǎn),以![]() 軸的正半軸為極軸,建立極坐標(biāo)系,曲線
軸的正半軸為極軸,建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程是
的極坐標(biāo)方程是![]() .
.
(1)寫(xiě)出直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)已知點(diǎn)![]() .若點(diǎn)
.若點(diǎn)![]() 的極坐標(biāo)為
的極坐標(biāo)為![]() ,直線
,直線![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() 且與曲線
且與曲線![]() 相交于
相交于![]() 兩點(diǎn),設(shè)線段
兩點(diǎn),設(shè)線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在北京召開(kāi)的國(guó)際數(shù)學(xué)家大會(huì)會(huì)標(biāo)如圖所示,它是由4個(gè)相同的直角三角形與中間的小正方形拼成的一大正方形,若直角三角形中較小的銳角為θ,大正方形的面積是1,小正方形的面積是 ![]() ,則sin2θ﹣cos2θ的值等于( )
,則sin2θ﹣cos2θ的值等于( ) 
A.1
B.﹣ ![]()
C.![]()
D.﹣ ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若存在實(shí)數(shù)![]() 和
和![]() ,使得函數(shù)
,使得函數(shù)![]() 和
和![]() 對(duì)定義域內(nèi)的任意
對(duì)定義域內(nèi)的任意![]() 均滿足:
均滿足:![]() ,且存在
,且存在![]() 使得
使得![]() ,存在
,存在![]() 使得
使得![]() ,則稱(chēng)直線
,則稱(chēng)直線![]() 為函數(shù)
為函數(shù)![]() 和
和![]() 的“分界線”.在下列說(shuō)法中正確的是__________(寫(xiě)出所有正確命題的編號(hào)).
的“分界線”.在下列說(shuō)法中正確的是__________(寫(xiě)出所有正確命題的編號(hào)).
①任意兩個(gè)一次函數(shù)最多存在一條“分界線”;
②“分界線”存在的兩個(gè)函數(shù)的圖象最多只有兩個(gè)交點(diǎn);
③![]() 與
與![]() 的“分界線”是
的“分界線”是![]() ;
;
④![]() 與
與![]() 的“分界線”是
的“分界線”是![]() 或
或![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知 ![]() =(
=( ![]() sinx,m+cosx),
sinx,m+cosx), ![]() =(cosx,﹣m+cosx),且f(x)=
=(cosx,﹣m+cosx),且f(x)= ![]()
(1)求函數(shù)f(x)的解析式;
(2)當(dāng)x∈[﹣ ![]() ,
, ![]() ]時(shí),f(x)的最小值是﹣4,求此時(shí)函數(shù)f(x)的最大值,并求出相應(yīng)的x的值.
]時(shí),f(x)的最小值是﹣4,求此時(shí)函數(shù)f(x)的最大值,并求出相應(yīng)的x的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某農(nóng)場(chǎng)計(jì)劃種植某種新作物,為此對(duì)這種作物的兩個(gè)品種(分別稱(chēng)為品種甲和品種乙)進(jìn)行田間試驗(yàn).選取兩大塊地,每大塊地分成![]() 小塊地,在總共
小塊地,在總共![]() 小塊地中,隨機(jī)選
小塊地中,隨機(jī)選![]() 小塊地種植品種甲,另外
小塊地種植品種甲,另外![]() 小塊地種植品種乙.
小塊地種植品種乙.
(1)假設(shè)![]() ,求第一大塊地都種植品種甲的概率;
,求第一大塊地都種植品種甲的概率;
(2)試驗(yàn)時(shí)每大塊地分成![]() 小塊,即
小塊,即![]() ,試驗(yàn)結(jié)束后得到品種甲和品種乙在各小塊地上的每公頃產(chǎn)量(單位:kg/hm2)如下表:
,試驗(yàn)結(jié)束后得到品種甲和品種乙在各小塊地上的每公頃產(chǎn)量(單位:kg/hm2)如下表:
甲 |
|
|
|
|
|
|
|
|
乙 |
|
|
|
|
|
|
|
|
分別求品種甲和品種乙的每公頃產(chǎn)量的樣本平均數(shù)和樣本方差;根據(jù)試驗(yàn)結(jié)果,你認(rèn)為應(yīng)該種植哪一品種?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四棱錐![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 上一點(diǎn),
上一點(diǎn), ![]() ,
, ![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).

(1)證明: ![]() 平面
平面![]() ;
;
(2)求異面直線![]() 與
與![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
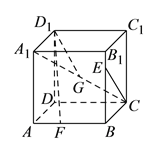
【題目】已知正方體![]() ,點(diǎn)
,點(diǎn)![]() ,
, ![]() ,
, ![]() 分別是線段
分別是線段![]() ,
, ![]() 和
和![]() 上的動(dòng)點(diǎn),觀察直線
上的動(dòng)點(diǎn),觀察直線![]() 與
與![]() ,
, ![]() 與
與![]() .給出下列結(jié)論:
.給出下列結(jié)論:
①對(duì)于任意給定的點(diǎn)![]() ,存在點(diǎn)
,存在點(diǎn)![]() ,使得
,使得![]() ;
;
②對(duì)于任意給定的點(diǎn)![]() ,存在點(diǎn)
,存在點(diǎn)![]() ,使得
,使得![]() ;
;
③對(duì)于任意給定的點(diǎn)![]() ,存在點(diǎn)
,存在點(diǎn)![]() ,使得
,使得![]() ;
;
④對(duì)于任意給定的點(diǎn)![]() ,存在點(diǎn)
,存在點(diǎn)![]() ,使得
,使得![]() .
.
其中正確結(jié)論的個(gè)數(shù)是( ).
A. ![]() 個(gè) B.
個(gè) B. ![]() 個(gè) C.
個(gè) C. ![]() 個(gè) D.
個(gè) D. ![]() 個(gè)
個(gè)
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com