
【題目】已知在平面直角坐標系中,圓![]() 的參數方程為
的參數方程為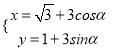 (
(![]() 為參數),以原點為極點,以
為參數),以原點為極點,以![]() 軸為非負半軸為極軸建立極坐標系.
軸為非負半軸為極軸建立極坐標系.
(1)求圓![]() 的普通方程與極坐標方程;
的普通方程與極坐標方程;
(2)若直線![]() 的極坐標方程為
的極坐標方程為![]() ,求圓
,求圓![]() 上的點到直線
上的點到直線![]() 的最大距離.
的最大距離.
科目:高中數學 來源: 題型:
【題目】哈三中群力校區高二、六班同學用隨機抽樣的辦法對所在校區老師的飲食習慣進行了一次調查, 飲食指數結果用莖葉圖表示如圖, 圖中飲食指數低于70的人,飲食以蔬菜為主;飲食指數高于70的人,飲食以肉類為主.

(1)完成下列![]() 列聯表:
列聯表:

能否有![]() 的把握認為老師的飲食習慣與年齡有關?
的把握認為老師的飲食習慣與年齡有關?
(2)從調查的結果中飲食指數在![]() 的老師內任選3名老師, 設“選到的三位老師飲食指數之和不超過105”為事件
的老師內任選3名老師, 設“選到的三位老師飲食指數之和不超過105”為事件![]() , 求事件
, 求事件![]() 發生的概率;
發生的概率;
(3)為了給食堂提供老師的飲食信息, 根據(1)的結論,能否有更好的抽樣方法來估計老師的飲食習慣, 并說明理由.
附:
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某賽季甲、乙兩名籃球運動員每場比賽得分的原始記錄如下:
甲運動員得分:13,51,23,8,26,38,16,33,14,28,39;
乙運動員得分:49,24,12,31,50,31,44,36,15,37,25,36,39.
(1)用十位數為莖,在答題卡中畫出原始數據的莖葉圖;
(2)用分層抽樣的方法在乙運動員得分十位數為 2,3,4 的比賽中抽取一個容量為 5 的樣本,從該樣本中隨機抽取 2 場,求其中恰有 1 場得分大于 40 分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() .
.
(1)求證:對![]() ,直線
,直線![]() 與圓
與圓![]() 總有兩個交點;
總有兩個交點;
(2)設直線![]() 與圓
與圓![]() 交于點
交于點![]() ,若
,若![]() ,直線
,直線![]() 的傾斜角;
的傾斜角;
(3)設直線![]() 與圓
與圓![]() 交于點
交于點![]() ,若定點
,若定點![]() 滿足
滿足![]() ,求此時直線
,求此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,圓
,圓![]() 過
過![]() 作圓
作圓![]() 的切線,切點為
的切線,切點為![]() (
(![]() 在第二象限).
在第二象限).
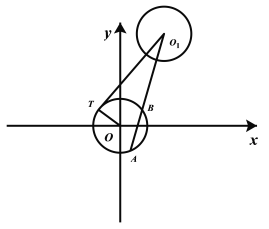
(1)求![]() 的正弦值;
的正弦值;
(2)已知點![]() ,過
,過![]() 點分別作兩圓切線,若切線長相等,求
點分別作兩圓切線,若切線長相等,求![]() 關系;
關系;
(3)是否存在定點![]() ,使過點
,使過點![]() 有無數對相互垂直的直線
有無數對相互垂直的直線![]() 滿足
滿足![]() ,且它們分別被圓
,且它們分別被圓![]() 、圓
、圓![]() 所截得的弦長相等?若存在,求出所有的點
所截得的弦長相等?若存在,求出所有的點![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD是正方形,![]() 平面ABCD,且
平面ABCD,且![]() ,點E為線段PD的中點.
,點E為線段PD的中點.
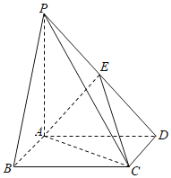
(1)求證:![]() 平面AEC;
平面AEC;
(2)求證:![]() 平面PCD;
平面PCD;
(3)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】語音交互是人工智能的方向之一,現在市場上流行多種可實現語音交互的智能音箱,它們可以通過語音交互滿足人們的部分需求.經市場調查,某種新型智能音箱的廣告費支出x(萬元)與銷售額y(單位:萬元)之間有如下對應數據:
x | 1 | 4 | 5 | 6 | 9 |
y | 20 | 35 | 50 | 65 | 80 |
(1)求y關于x的線性回歸方程(數據精確到0.01);
(2)利用(1)中的回歸方程,預測廣告費支出10萬元時的銷售額.
附:回歸直線的斜率和截距的最小二乘估計公式分別為: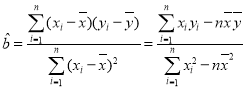 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
, ![]() .
.
(1)若函數![]() 在
在![]() 上單調遞增,求
上單調遞增,求![]() 的取值范圍;
的取值范圍;
(2)設![]() ,點
,點![]() 是曲線
是曲線![]() 與
與![]() 的一個交點,且這兩曲線在點
的一個交點,且這兩曲線在點![]() 處的切線互相垂直,證明:存在唯一的實數
處的切線互相垂直,證明:存在唯一的實數![]() 滿足題意,且
滿足題意,且![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com