【題目】為了解某校高三學生的視力情況，隨機地抽查了該校1000名高三學生的視力情況，得到頻率分布直方圖，如圖，由于不慎將部分數據丟失，但知道前4組的頻數成等比數列，后6組的頻數成等差數列，設最大頻率為
，視力在4.6到5.0之間的學生數
， 
的值分別為（ ）
A. 
B. 
C. 
D. 
百年學典課時學練測系列答案科目：高中數學 來源： 題型：
【題目】某市將建一個制藥廠，但該廠投產后預計每天要排放大約80噸工業廢氣，這將造成極大的環境污染.為了保護環境，市政府決定支持該廠貸款引進廢氣處理設備來減少廢氣的排放，該設備可以將廢氣轉化為某種化工產品和符合排放要求的氣體，經測算，制藥廠每天利用設備處理廢氣的綜合成本
（元）與廢氣處理量
（噸）之間的函數關系可近似地表示為
，且每處理
噸工業廢氣可得價值為
元的某種化工產品并將之利潤全部用來補貼廢氣處理.
（1）若該制藥廠每天廢氣處理量計劃定位20噸時，那么工廠需要每天投入的廢氣處理資金為多少元？
（2）若該制藥廠每天廢氣處理量計劃定為
噸，且工廠不用投入廢氣處理資金就能完成計劃的處理量，求
的取值范圍；
（3）若該制藥廠每天廢氣處理量計劃定為
（
）噸，且市政府決定為處理每噸廢氣至少補貼制藥廠
元以確保該廠完成計劃的處理量總是不用投入廢氣處理資金，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修
：不等式選講
已知函數f（x）=|2x+3|+|2x﹣1|．
（Ⅰ）求不等式f（x）＜8的解集；
（Ⅱ）若關于x的不等式f（x）≤|3m+1|有解，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2017屆廣西陸川縣中學高三文上學期二模】已知函數
.
（I）求函數
的單調區間；
（II）若
在
上恒成立，求實數
的取值范圍；
（III）在（II）的條件下，對任意的
，求證：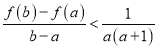
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，(
)．
（1）若函數
與
的圖象在
上有兩個不同的交點，求實數
的取值范圍；
（2）若在
上不等式
恒成立，求實數的取值范圍；
（3）證明：對于
時，任意
，不等式
恒成立．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分，第（1）問 6 分，第（2）問 6 分）
某品牌新款夏裝即將上市，為了對夏裝進行合理定價，在該地區的三家連鎖店各進行了兩天試銷售，得到如下數據：
連鎖店 | A店 | B店 | C店 | |||
售價 | 80 | 86 | 82 | 88 | 84 | 90 |
銷售量 | 88 | 78 | 85 | 75 | 82 | 66 |
（1）以三家連鎖店分別的平均售價和平均銷量為散點，求出售價與銷量的回歸直線方程
；
（2）在大量投入市場后，銷售量與單價仍然服從（1）中的關系，且該夏裝成本價為40元/件，為使該款夏裝在銷售上獲得最大利潤，該款夏裝的單價應定為多少元（保留整數）？
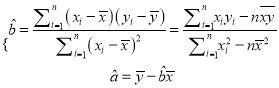
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
，
.
（Ⅰ）若
恒成立，求
的取值范圍；
（Ⅱ）設
，
，（
為自然對數的底數）.是否存在常數
，使
恒成立，若存在，求出的取值范圍；若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
