【題目】一份測試題包括6道選擇題，每題只有一個選項是正確的．如果一個學生對每一道題都隨機猜一個答案，用隨機模擬方法估計該學生至少答對3道題的概率．
【答案】0.16
【解析】試題分析：利用計算機或計算器可以產生0到3之間取整數值的隨機數．我們用0表示猜的選項正確，1,2,3表示猜的選項錯誤，將6個隨機數當做一組，產生25組隨機數，相當于做了25次實驗，數出其中大于等于3個0的數組，除以25就是估計的概率。
我們通過設計模擬試驗的方法來解決問題．利用計算機或計算器可以產生0到3之間取整數值的隨機數．我們用0表示猜的選項正確，1,2,3表示猜的選項錯誤，這樣可以體現猜對的概率是25%.因為共猜6道題，所以每6個隨機數作為一組．例如，產生25組隨機數：
330130 302220 133020 022011 313121 222330
231022 001003 213322 030032 100211 022210
231330 321202 031210 232111 210010 212020
230331 112000 102330 200313 303321 012033
321230
就相當于做了25次試驗，在每組數中，如果恰有3個或3個以上的數是0，則表示至少答對3道題，它們分別是001003,030032,210010,112000，即共有4組數，我們得到該同學6道選擇題至少答對3道題的概率近似為
＝0.16.
科目：高中數學 來源： 題型：
【題目】宿州市教體局為了了解
屆高三畢業生學生情況，利用分層抽樣抽取
位學生數學學業水平測試成績作調查，制作了成績頻率分布直方圖，如圖所示，其中成績分組區間是：
，
，
，
，
，
.
（Ⅰ）求圖中
的值；
（Ⅱ）根據直方圖估計宿州市屆高三畢業生數學學業水平測試成績的平均分；
（Ⅲ）在抽取的人中，從成績在和
的學生中隨機選取
人，求這人成績差別不超過
分的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量
，
為坐標原點，動點
滿足：
．
（Ⅰ）求動點的軌跡
的方程；
（Ⅱ）已知直線
都過點
，且
，
與軌跡分別交于點
，試探究是否存在這樣的直線？使得
是等腰直角三角形．若存在，指出這樣的直線共有幾組（無需求出直線的方程）；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種商品在
天每件的銷售價格
（元）與時間
（天）的函數關系用如圖表示，該商品在
天內日銷售量
（件）與時間
（天）之間的關系如下表：
|
|
|
|
|
|
|
|
|
|
（
）根據提供的圖象（如圖），寫出該商品每件的銷售價格
與時間
的函數關系式.
（
）根據表
提供的數據，寫出日銷售量
與時間
的一次函數關系式.
（
）求該商品的日銷售金額的最大值，并指出日銷售金額最大的一天是
天中的第幾天.（日銷售金額
每件的銷售價格
日銷售量）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著移動互聯網時代的到來，手機的使用非常普遍，“低頭族”隨處可見。某校為了解家長和教師對學生帶手機進校園的態度，隨機調查了100位家長和教師，得到情況如下表：
教師 | 家長 | |
反對 | 40 | 20 |
支持 | 20 | 20 |
（1）是否有95%以上的把握認為“帶手機進校園與身份有關”，并說明理由；
（2）把以上頻率當概率，隨機抽取3位教師，記其中反對學生帶手機進校園的人數為X，求隨機變量X的分布列和數學期望．
附：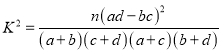 
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2014課標全國Ⅰ，文12】已知函數f(x)＝ax3－3x2＋1，若f(x)存在唯一的零點x0，且x0＞0，則a的取值范圍是( )．
A．(2，＋∞) B．(1，＋∞)
C．(－∞，－2) D．(－∞，－1)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解某校高三學生的視力情況，隨機地抽查了該校1000名高三學生的視力情況，得到頻率分布直方圖，如圖，由于不慎將部分數據丟失，但知道前4組的頻數成等比數列，后6組的頻數成等差數列，設最大頻率為
，視力在4.6到5.0之間的學生數
， 
的值分別為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】交強險是車主必須為機動車購買的險種，若普通6座以下私家車投保交強險第一年的費用（基準保費）統一為
元，在下一年續保時，實行的是費率浮動機制，保費與上一年度車輛發生道路交通事故的情況相聯系，發生交通事故的次數越多，費率也就是越高，具體浮動情況如下表：
交強險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
| 上一個年度未發生有責任道路交通事故 | 下浮10% |
| 上兩個年度未發生有責任道路交通事故 | 下浮20% |
| 上三個及以上年度未發生有責任道路交通事故 | 下浮30% |
| 上一個年度發生一次有責任不涉及死亡的道路交通事故 | 0% |
| 上一個年度發生兩次及兩次以上有責任道路交通事故 | 上浮10% |
| 上一個年度發生有責任道路交通死亡事故 | 上浮30% |
某機構為了 某一品牌普通6座以下私家車的投保情況，隨機抽取了60輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況，統計得到了下面的表格：
類型 |
|
|
|
|
|
|
數量 | 10 | 5 | 5 | 20 | 15 | 5 |
以這60輛該品牌車的投保類型的頻率代替一輛車投保類型的概率，完成下列問題：
（1）按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規定，
，記
為某同學家的一輛該品牌車在第四年續保時的費用，求的分布列與數學期望；（數學期望值保留到個位數字）
（2）某二手車銷售商專門銷售這一品牌的二手車，且將下一年的交強險保費高于基本保費的車輛記為事故車，假設購進一輛事故車虧損5000元，一輛非事故車盈利10000元：
①若該銷售商購進三輛（車齡已滿三年）該品牌二手車，求這三輛車中至多有一輛事故車的概率；
②若該銷售商一次購進100輛（車齡已滿三年）該品牌二手車，求他獲得利潤的期望值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
