
分析 (1)利用向量的數量積以及兩角和與差的三角函數化簡函數的解析式,利用正弦函數的單調區間求解即可.
(2)利用(1)化簡函數的表達式,通過二倍角公式求解即可.
解答 解:(1)∵向量$\vec a=(1,cos2x),\vec b=(sin2x,-\sqrt{3})$,
∴$f(x)=\vec a•\vec b=sin2x-\sqrt{3}cos2x=2sin(2x-\frac{π}{3})$.-----(3分)
令$2kπ-\frac{π}{2}≤2x-\frac{π}{3}≤2kπ+\frac{π}{2}$得:$kπ-\frac{π}{12}≤x≤kπ+\frac{5π}{12}$(k∈Z)
∴函數f(x)的單調增區間為$[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}]$(k∈Z).-----(6分)
(2)∵$f(\frac{θ}{2}+\frac{2π}{3})=2sin(θ+\frac{4π}{3}-\frac{π}{3})=-2sinθ=\frac{6}{5}$,∴$sinθ=-\frac{3}{5}$.-----(10分)
∴$cos2θ=1-2{sin^2}θ=1-2×\frac{9}{25}=\frac{7}{25}$.-----(12分)
點評 本題考查向量的數量積的運算,兩角和與差的三角函數,考查計算能力.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 大前提錯導致結論錯 | B. | 小前提錯導致結論錯 | ||
| C. | 推理形式錯導致結論錯 | D. | 大前提和小前提錯導致結論錯 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | -$\frac{9}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
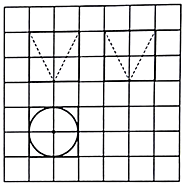 如圖,網格紙上小正方形的邊長為1,粗實線畫出的是某幾何體的三視圖,則該幾何體的表面積為( )
如圖,網格紙上小正方形的邊長為1,粗實線畫出的是某幾何體的三視圖,則該幾何體的表面積為( )| A. | $20+\sqrt{5}π$ | B. | $24+\sqrt{5}π$ | C. | $20+(\sqrt{5}-1)π$ | D. | $24+(\sqrt{5}-1)π$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({3,\frac{201}{10}})$ | B. | $({1,\frac{181}{10}})$ | C. | $({2\sqrt{2},+∞})$ | D. | $({2\sqrt{2}-2,+∞})$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com