定義在R上的函數f(x)滿足:f(m+n)=f(m)+f(n)-2對任意m、n∈R恒成立,當x>0時,f(x)>2.
(Ⅰ) 求證f(x)在R上是單調遞增函數;
(Ⅱ)已知f(1)=5,解關于t的不等式f(|t2-t|)≤8;
(Ⅲ)若f(-2)=-4,且不等式f(t2+at-a)≥-7對任意t∈[-2,2]恒成立.求實數a的取值范圍.
【答案】
分析:(Ⅰ)結合已知先構造x
2-x
1>0,可得f(x
2-x
1)>2,利用函數的單調性的定義作差f(x
1)-f(x
2)變形可證明
(Ⅱ)由f(1),及f(2)=f(1)+f(1)-2可求f(2),然后結合(I)中的函數的單調性可把已知不等式進行轉化,解二次不等式即可
(Ⅲ)由f(-2)及已知可求f(-1),進而可求f(-3),由已知不等式及函數的單調性可轉化原不等式,結合恒成立與最值求解的相互轉化即可求解
解答:證明:(Ⅰ)?x
1,x
2∈R,當x
1<x
2時,x
2-x
1>0,
∴f(x
2-x
1)>2f(x
1)-f(x
2)
=f(x
1)-f(x
2-x
1+x
1)
=f(x
1)-f(x
2-x
1)-f(x
1)+2
=2-f(x
2-x
1)<0,
所以f(x
1)<f(x
2),
所以f(x)在R上是單調遞增函數…(4分)
(Ⅱ)∵f(1)=5,
∴f(2)=f(1)+f(1)-2=8,
由f(|t
2-t|)≤8得f(|t
2-t|)≤f(2)
∵f(x)在R上是單調遞增函數,所以
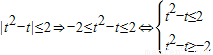
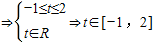
…(8分)
(Ⅲ)由f(-2)=-4得-4=f(-2)=f(-1)+f(-1)-2⇒f(-1)=-1
所以f(-3)=f(-2)+f(-1)=-4-1-2=-7,
由f(t
2+at-a)≥-7得f(t
2+at-a)≥f(-3)
∵f(x)在R上是單調遞增函數,
所以t
2+at-a≥-3⇒t
2+at-a+3≥0對任意t∈[-2,2]恒成立.
記g(t)=t
2+at-a+3(-2≤t≤2)
只需g
min(t)≥0.對稱軸
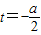
(1)當
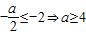
時,
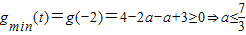
與a≥4矛盾.
此時a∈ϕ
(2)當
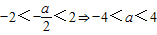
時,
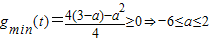
,
又-4<a<4,所以-4<a≤2
(3)當
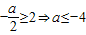
時,g
min(t)=g(2)=4+2a-a+3≥0⇒a≥-7
又a≤-4
∴-7≤a≤-4
綜合上述得:a∈[-7,2]…(14分)
點評:本題主要考查了賦值法在抽象函數的函數值的求解中的應用,抽象函數的單調性的證明及函數的恒成立問題的應用,具有很強的綜合性

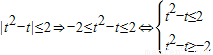
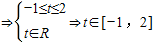 …(8分)
…(8分)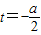
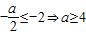 時,
時,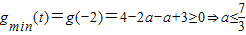 與a≥4矛盾.
與a≥4矛盾.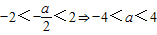 時,
時,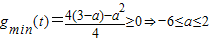 ,
,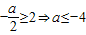 時,gmin(t)=g(2)=4+2a-a+3≥0⇒a≥-7
時,gmin(t)=g(2)=4+2a-a+3≥0⇒a≥-7
