Question

【題目】已知函數， ，其中為自然對數的底數.

（Ⅰ）求曲線在點處的切線方程；

（Ⅱ）若對任意，不等式恒成立，求實數的取值范圍；

（Ⅲ）試探究當時，方程的解的個數，并說明理由.

Answer 1

【答案】(Ⅰ) ；(Ⅱ) ；(Ⅲ)答案見解析.

【解析】試題分析：本題主要考查導數的運算、利用導數判斷函數的單調性、利用導數求函數的切線方程、利用導數求函數的最值等基礎知識，考查學生的分析問題解決問題的能力、轉化能力、計算能力.第一問，先利用誘導公式化簡，再對求導， 為切點的縱坐標， 為切線的斜率，最后利用點斜式求曲線的切線；第二問，將對任意，不等式恒成立，轉化為， 構造函數對求導，判斷函數的單調性，求最小值，代入到中即可；第三問，分情況討論，對求導，利用導數判斷函數的單調性，再驗證區間端點縱坐標的正負來決定函數的一個零點.

試題解析：（1）依題意得， ，

.

所以曲線在點處的切線方程為. 4分

（2）等價于對任意， .5分

設， ．

則

因為，所以，

所以，故在單調遞增， 6分

因此當時，函數取得最小值； 7分

所以，即實數的取值范圍是.8分

（3）設， ．

①當時，由（2）知，函數在單調遞增，

故函數在至多只有一個零點，

又，而且函數圖象在上是連續不斷的，

因此，函數在上有且只有一個零點.10分

②當時， 恒成立．證明如下：

設，則，所以在上單調遞增，

所以時， ，所以，

又時， ，所以，即，即．

故函數在上沒有零點.11分

③當時， ，所以函數在上單調遞減，故函數在至多只有一個零點，

又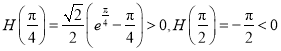，而且函數在上是連續不斷的，

因此，函數在上有且只有一個零點.13分

綜上所述， 時，方程有兩個解.14分