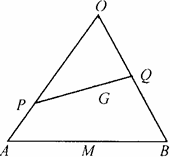
日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

如圖所示，設G為△OAB的重心，過G的直線與OA，OB分別交于P和Q，已知，，△OAB與△OPQ的面積分別為S和T．求證：

(1)；

(2)．

答案：
解析：

證明(1)聯結OG并延長交AB于M，則M為AB的中點，

∴，

．　　　　　　　　　　①

設G分PQ所成比為t：(1－t)，則，

而，，∴　　②

比較①，②得

，，即，，　∴．

(2)∵∠POQ=∠AOB，∴．

由題(1)知，3h－1>0，∴．

又，

，且依題意0<h≤1，0<k≤1，

∴，∴，．

因此，成立．


練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

如圖所示的集合體是將高為2，底面半徑為1的直圓柱沿過軸的平面切開后，將其中一半沿切面向右水平平移后得到的．A，A′，B，B′分別為
CD
，
C′D′
，
DE
，
D′E′
的中點，O1，
O
′
1
，O2，
O
′
2
分別為CD，C′D′，DE，D′E′的中點．
（1）證明：
O
′
1
，A′，O2，B四點共面；
（2）設G為A A′中點，延長A′
O
′
1
到H′，使得
O
′
1
H′=A′
O
′
1
．證明：B
O
′
2
⊥平面H′B′G′．

查看答案和解析>>

科目：高中數學 來源：不詳 題型：解答題

如圖所示的集合體是將高為2，底面半徑為1的直圓柱沿過軸的平面切開后，將其中一半沿切面向右水平平移后得到的．A，A′，B，B′分別為








CD
，








C′D′
，








DE
，








D′E′
的中點，O1，
O′1
，O2，
O′2
分別為CD，C′D′，DE，D′E′的中點．
（1）證明：
O′1
，A′，O2，B四點共面；
（2）設G為A A′中點，延長A′
O′1
到H′，使得
O′1
H′=A′
O′1
．證明：B
O′2
⊥平面H′B′G′．
精英家教網

查看答案和解析>>

科目：高中數學 來源： 題型：

如圖所示，已知兩動點P、Q依次在兩條射線x+y=0(x＞0),x-y=0(x＞0)上，△POQ的面積為定值4（O為坐標原點），設G是△POQ的重心，求|OG|的最小值.

查看答案和解析>>

科目：高中數學 來源： 題型：

以O為原點，所在的直線為x軸，建立如圖所示的直角坐標系.設·=1，點F的坐標為(t，0)，t∈［3，+∞)，點G的坐標為(x0，y0).

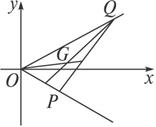
(1)求x0關于t的函數x0=f(x)的表達式，判斷函數f(t)的單調性，并證明你的判斷；

(2)設△OFG的面積S=t，若以O為中心，F為焦點的橢圓經過點G，求當||取得最小值時橢圓的方程；

(3)在(2)的條件下，若點P的坐標為(0，92)，C、D是橢圓上的兩點，且=λ(λ≠1)，求實數λ的取值范圍.

查看答案和解析>>

科目：高中數學 來源： 題型：

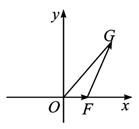
以O為原點,以所在直線為x軸,建立如圖所示的直角坐標系.設·=1,點F的坐標為(t,0),t∈［3,+∞),點G的坐標為(x0,y0).

(1)求x0關于t的函數x0=f(t)的表達式,判斷函數f(t)的單調性,并證明你的判斷;

(2)設△OFG的面積S=t,若以O為中心、F為焦點的橢圓經過點G,求當||取得最小值時橢圓的方程.

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 亚洲精品一二三区 | 欧美在线一区二区三区 | 久久久精品日韩 | 91精品国产综合久久蜜臀 | 日韩在线免费电影 | 另类综合在线 | 中文字幕第66页 | 在线免费国产 | 久草视| 日韩精品一区二 | 狠狠操狠狠操 | 久久国产欧美日韩精品 | 免费大片在线观看网站 | a级毛片基地 | 国产在线一区二区三区在线观看 | 欧美视频在线免费看 | 亚洲人成在线观看 | 久久久久久久久久影院 | 一区二区精品视频 | 欧美一区二区视频在线观看 | 日韩极品在线 | 在线免费观看黄 | 免费的黄色 | 免费成人av在线 | 久久国产精品久久精品 | 天堂新版8中文在线8 | 一区二区三区四区在线 | 欧美不卡一区二区三区 | 日韩国产精品视频 | 资源av | 国产在线成人 | 精品免费国产一区二区三区 | 欧美盗摄 | 91综合视频在线观看 | 久久精品免费观看视频 | 国产成人免费观看 | 欧美一级网站 | 最新久久精品 | 欧美一区精品 | 免费黄色在线网址 | 2019亚洲日韩新视频 |