【題目】已知向量
為正實數， 
.
(1)若
，求
的最大值；
(2)是否存在
，使
？若存在，求出
的取值范圍；若不存在，請說明理由．
【答案】（1）
；（2）不存在
，使
.
【解析】試題分析：（1）若
⊥
，則
·
＝0，即(－2t2－1)(－
－
)＋(t2＋3)(－
＋
)＝0，得k＝
＝
≤
，從而得解；
（2）假設存在正實數k，t，使
∥
，則(－2t2－1)(－
＋
)－(t2＋3)(－
－
)＝0，整理得t3＋t＋k＝0，從而得解.
試題解析：
＝(1,2)＋(t2＋1)(－2,1)＝(－2t2－1，t2＋3)， 
＝(－
－
，－ 
＋
)．
(1)若
⊥
，則
·
＝0，即(－2t2－1)(－
－
)＋(t2＋3)(－
＋
)＝0，
整理得，k＝
＝
≤
，當且僅當
，即t＝1時取等號，∴kmax＝
.
(2)假設存在正實數k，t，使
∥
，則(－2t2－1)(－
＋
)－(t2＋3)(－
－
)＝0，化簡得
＝0，即t3＋t＋k＝0.
因為k，t是正實數，故滿足上式的k，t不存在，所以不存在k，t，使
∥
.
小學同步三練核心密卷系列答案科目：高中數學 來源： 題型：
【題目】某網站從春節期間參與收發網絡紅包的手機用戶中隨機抽取
名進行調查，將受訪用戶按年齡分成
組： 
， 
，…， 
，并整理得到如下頻率分布直方圖：
（Ⅰ）求
的值；
（Ⅱ）從春節期間參與收發網絡紅包的手機用戶中隨機抽取一人，估計其年齡低于
歲的概率；
（Ⅲ）估計春節期間參與收發網絡紅包的手機用戶的平均年齡．
查看答案和解析>>
科目：高中數學 來源： 題型：
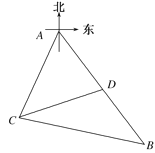
【題目】某觀測站
在目標
的南偏西
方向，從
出發有一條南偏東
走向的公路，在
處測得與
相距
的公路
處有一個人正沿著此公路向
走去，走
到達
，此時測得
距離為
，若此人必須在
分鐘內從
處到達
處，則此人的最小速度為( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
.
（1）求函數
的圖象在
處的切線方程；
（2）若函數
在
上有兩個不同的零點，求實數
的取值范圍；
（3）是否存在實數
，使得對任意的
，都有函數
的圖象在
的圖象的下方？若存在，請求出最大整數
的值；若不存在，請說理由.
（參考數據： 
， 
）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐P—ABCD的底面ABCD是正方形，側棱PD⊥底面ABCD，PD=DC，E是PC的中點．
（Ⅰ）證明PA//平面BDE；
（Ⅱ）求二面角B—DE—C的平面角的余弦值；
（Ⅲ）在棱PB上是否存在點F，使PB⊥平面DEF？證明你的結論．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校為了解本校學生網課期間課后玩電腦游戲時長情況，隨機抽取了100名學生進行調查．下面是根據調查結果繪制的學生每天玩電腦游戲的時長的頻率分布直方圖．
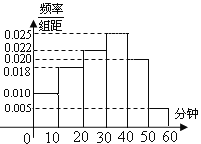
（1）根據頻率分布直方圖估計抽取樣本的平均數
（同一組中的數據用該組區間的中點值作代表）；
（2）已知樣本中玩電腦游戲時長在
的學生中，男生比女生多1人，現從中任選3人進行回訪，求選出的3人中恰有兩人是男生的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某一部件由四個電子元件按如圖方式連接而成，元件1或元件2正常工作，且元件3或元件4正常工作，則部件正常工作.設四個電子元件的使用壽命（單位：小時）均服從正態分布
，且各個元件能否正常工作相互獨立，那么該部件的使用壽命超過1000小時的概率為__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】機床廠今年年初用98萬元購進一臺數控機床，并立即投入生產使用，計劃第一年維修、保養費用12萬元，從第二年開始，每年所需維修、保養費用比上一年增加4萬元，該機床使用后，每年的總收入為50萬元，設使用x年后數控機床的盈利額為y萬元．
(Ⅰ)寫出y與x之間的函數關系式；
(Ⅱ)從第幾年開始，該機床開始盈利（盈利額為正值）；
(Ⅲ)使用若干年后，對機床的處理方案有兩種：
(1)當年平均盈利額達到最大值時，以30萬元價格處理該機床；
(2)當盈利額達到最大值時，以12萬元價格處理該機床．
請你研究一下哪種方案處理較為合理？請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
