
分析 利用分離常數法求解即可.
解答 解:∵函數f(x)的定義域為{x∈R|x≠1}
函數f(x)=$\frac{3x+1}{x-1}$=$\frac{3(x-1)+4}{x-1}$=$3+\frac{4}{x-1}$;
∵$\frac{4}{x-1}$≠0,
∴f(x)≠3
所以函數f(x)的值域是(-∞,3)∪(3,+∞)
故答案為:(-∞,3)∪(3,+∞)
點評 本題考查了函數值域的求法.高中函數值域求法有:1、觀察法,2、配方法,3、反函數法,4、判別式法;5、換元法,6、數形結合法,7、不等式法,8、分離常數法,9、單調性法,10、利用導數求函數的值域,11、最值法,12、構造法,13、比例法.要根據題意選擇.


科目:高中數學 來源: 題型:選擇題
| A. | $(-∞,-\frac{1}{8}]$ | B. | $(-∞,-\frac{1}{8}]∪[1,+∞)$ | C. | [1,+∞) | D. | $[-\frac{1}{8},\;1]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1)(3)(4) | B. | (1)(2) | C. | (3)(4) | D. | (2)(3)(4) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
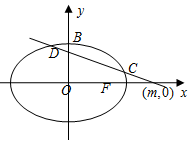 如圖,已知圓G:x2+y2-2x-$\sqrt{2}$y=0經過橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點F及上頂點B,過橢圓外一點(m,0)(m>a)且傾斜角為$\frac{5}{6}$π的直線l交橢圓于C,D兩點.
如圖,已知圓G:x2+y2-2x-$\sqrt{2}$y=0經過橢圓$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦點F及上頂點B,過橢圓外一點(m,0)(m>a)且傾斜角為$\frac{5}{6}$π的直線l交橢圓于C,D兩點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 6$\sqrt{3}$ | B. | 6 | C. | 12 | D. | 12$\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com