
【題目】某地區有800名學員參加交通法規考試,考試成績的頻率分布直方圖如圖所示,其中成績分組區間是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,規定90分及以上為合格:
,規定90分及以上為合格:
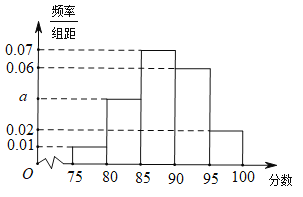
(1)求圖中a的值;
(2)根據頻率分布直方圖估計該地區學員交通法規考試合格的概率;
(3)若三個人參加交通法規考試,估計這三個人至少有兩人合格的概率.
 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:
【題目】設橢圓![]() ,定義橢圓C的“相關圓”E為:
,定義橢圓C的“相關圓”E為:![]() .若拋物線
.若拋物線![]() 的焦點與橢圓C的右焦點重合,且橢圓C的短軸長與焦距相等.
的焦點與橢圓C的右焦點重合,且橢圓C的短軸長與焦距相等.
(1)求橢圓C及其“相關圓”E的方程;
(2)過“相關圓”E上任意一點P作其切線l,若l 與橢圓![]() 交于A,B兩點,求證:
交于A,B兩點,求證:![]() 為定值(
為定值(![]() 為坐標原點);
為坐標原點);
(3)在(2)的條件下,求![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某沿海城市的海邊有兩條相互垂直的直線型公路l1、l2,海岸邊界MPN近似地看成一條曲線段.為開發旅游資源,需修建一條連接兩條公路的直線型觀光大道AB,且直線AB與曲線MPN有且僅有一個公共點P(即直線與曲線相切),如圖所示.若曲線段MPN是函數![]() 圖象的一段,點M到l1、l2的距離分別為8千米和1千米,點N到l2的距離為10千米,以l1、l2分別為x、y軸建立如圖所示的平面直角坐標系xOy,設點P的橫坐標為p.
圖象的一段,點M到l1、l2的距離分別為8千米和1千米,點N到l2的距離為10千米,以l1、l2分別為x、y軸建立如圖所示的平面直角坐標系xOy,設點P的橫坐標為p.
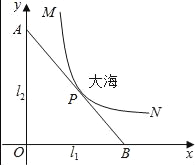
(1)求曲線段MPN的函數關系式,并指出其定義域;
(2)若某人從點O沿公路至點P觀景,要使得沿折線OAP比沿折線OBP的路程更近,求p的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 的首項為p,公差為
的首項為p,公差為![]() ,對于不同的自然數
,對于不同的自然數![]() ,直線
,直線![]() 與
與![]() 軸和指數函數
軸和指數函數![]() 的圖象分別交于點
的圖象分別交于點![]() 與
與![]() (如圖所示),記
(如圖所示),記![]() 的坐標為
的坐標為![]() ,直角梯形
,直角梯形![]() 、
、![]() 的面積分別為
的面積分別為![]() 和
和![]() ,一般地記直角梯形
,一般地記直角梯形![]() 的面積為
的面積為![]() .
.

(1)求證:數列![]() 是公比絕對值小于1的等比數列;
是公比絕對值小于1的等比數列;
(2)設![]() 的公差
的公差![]() ,是否存在這樣的正整數
,是否存在這樣的正整數![]() ,構成以
,構成以![]() ,
,![]() ,
,![]() 為邊長的三角形?并請說明理由;
為邊長的三角形?并請說明理由;
(3)設![]() 的公差
的公差![]() 為已知常數,是否存在這樣的實數p使得(1)中無窮等比數列
為已知常數,是否存在這樣的實數p使得(1)中無窮等比數列![]() 各項的和
各項的和![]() ?并請說明理由.
?并請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,若存在常數
,若存在常數![]() ,對任意
,對任意![]() 都有
都有![]() ,則稱函數
,則稱函數![]() 為T倍周期函數.
為T倍周期函數.
(1)判斷![]() 是否是T倍周期函數,并說明理由;
是否是T倍周期函數,并說明理由;
(2)證明 是T倍周期函數,且T的值是唯一的;
是T倍周期函數,且T的值是唯一的;
(3)若![]() 是2倍周期函數,
是2倍周期函數,![]() ,
,![]() ,
,![]() 表示
表示![]() 的前n項和,
的前n項和,![]() ,若
,若![]() 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,![]() 、
、![]() 是兩個垃圾中轉站,
是兩個垃圾中轉站,![]() 在
在![]() 的正東方向
的正東方向![]() 千米處,
千米處,![]() 的南面為居民生活區.為了妥善處理生活垃圾,政府決定在
的南面為居民生活區.為了妥善處理生活垃圾,政府決定在![]() 的北面建一個垃圾發電廠
的北面建一個垃圾發電廠![]() .垃圾發電廠
.垃圾發電廠![]() 的選址擬滿足以下兩個要求(
的選址擬滿足以下兩個要求(![]() 、
、![]() 、
、![]() 可看成三個點):①垃圾發電廠到兩個垃圾中轉站的距離與它們每天集中的生活垃圾量成反比,比例系數相同;②垃圾發電廠應盡量遠離居民區(這里參考的指標是點
可看成三個點):①垃圾發電廠到兩個垃圾中轉站的距離與它們每天集中的生活垃圾量成反比,比例系數相同;②垃圾發電廠應盡量遠離居民區(這里參考的指標是點![]() 到直線
到直線![]() 的距離要盡可能大).現估測得
的距離要盡可能大).現估測得![]() 、
、![]() 兩個中轉站每天集中的生活垃圾量分別約為
兩個中轉站每天集中的生活垃圾量分別約為![]() 噸和
噸和![]() 噸.設
噸.設![]() .
.
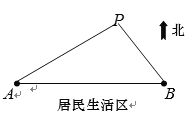
(1)求![]() (用
(用![]() 的表達式表示);
的表達式表示);
(2)垃圾發電廠該如何選址才能同時滿足上述要求?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 圖象上不同兩點
圖象上不同兩點![]() ,
,![]() ,
,![]() ,
,![]() 處的切線的斜率分別是
處的切線的斜率分別是![]() ,
,![]() ,規定
,規定![]() 叫曲線
叫曲線![]() 在點
在點![]() 與點
與點![]() 之間的“彎曲度”,給出以下命題:
之間的“彎曲度”,給出以下命題:
(1)函數![]() 圖象上兩點
圖象上兩點![]() 、
、![]() 的橫坐標分別為1,2,則
的橫坐標分別為1,2,則![]() ;
;
(2)存在這樣的函數,圖象上任意兩點之間的“彎曲度”為常數;
(3)設點![]() 、
、![]() 是拋物線,
是拋物線,![]() 上不同的兩點,則
上不同的兩點,則![]() ;
;
(4)設曲線![]() 上不同兩點
上不同兩點![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 恒成立,則實數
恒成立,則實數![]() 的取值范圍是
的取值范圍是![]() ;
;
以上正確命題的序號為__(寫出所有正確的)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)當a>0時,求函數f(x)的單調區間;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一件剛出土的珍貴文物要在博物館大廳中央展出,需要設計各面是玻璃平面的無底正四棱柱將其罩住,罩內充滿保護文物的無色氣體.已知文物近似于塔形,高1.8米,體積0.5立方米,其底部是直徑為0.9米的圓形,要求文物底部與玻璃罩底邊至少間隔0.3米,文物頂部與玻璃罩上底面至少間隔0.2米,氣體每立方米1000元,則氣體費用最少為( )元

A.4500B.4000C.2880D.2380
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com