
【題目】已知數列![]() 各項均為正數,其前
各項均為正數,其前![]() 項和為
項和為![]() ,且
,且![]() ,
, ![]() .
.![]()
(Ⅰ)求數列![]() 的通項公式;
的通項公式;
(Ⅱ)求數列![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】試題分析:(1)由![]() 當
當![]() 時,,
時,, ![]() ,兩式相減可得
,兩式相減可得![]() ,由此可得數列
,由此可得數列![]() 是公差為
是公差為![]() 的等差數列,從而能求出
的等差數列,從而能求出![]() ;(2)由
;(2)由![]() ,利用錯位相減法能求出數列
,利用錯位相減法能求出數列![]() 的前
的前![]() 項和.
項和.
試題解析:(Ⅰ)∵數列![]() 各項均為正數,其前
各項均為正數,其前![]() 項和為
項和為![]() ,且
,且![]() ,
, ![]() .
.![]() ,
,
∴當![]() 時,
時, ![]() ,解得
,解得![]() ,
,
當![]() 時,
時, ![]() ,
, ![]()
∵![]() ,∴
,∴![]() ,
,
∴![]() ,
, ![]() ,…,
,…, ![]() ,…,是以1為首項,2為公差的等差數列,
,…,是以1為首項,2為公差的等差數列, ![]() ,
,
![]() ,
, ![]() ,…,
,…, ![]() ,…,是以2為首項,2為公差的等差數,
,…,是以2為首項,2為公差的等差數, ![]() ,∴
,∴![]() ,
, ![]() .
.
(Ⅱ)∵![]() ,
, ![]() ,
,
∴數列![]() 的前
的前![]() 項和:
項和:
![]() ,①
,①
![]() ,②.
,②.
②-①,得: ![]()
![]()
![]() .
.
【易錯點晴】本題主要考查遞推公式、等差數列的通項公式、“錯位相減法”求數列的和,屬于難題. “錯位相減法”求數列的和是重點也是難點,利用“錯位相減法”求數列的和應注意以下幾點:①掌握運用“錯位相減法”求數列的和的條件(一個等差數列與一個等比數列的積);②相減時注意最后一項 的符號;③求和時注意項數別出錯;④最后結果一定不能忘記等式兩邊同時除以![]() .
.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)的圖象關于y軸對稱,并且是[0,+∞)上的減函數,若f(lgx)>f(1),則實數x的取值范圍是( )
A.![]()
B.![]()
C.![]()
D.(0,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電視傳媒公司為了了解某地區電視觀眾對某體育節目的收視情況,隨機抽取了100名觀眾進行調查,下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖:
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”.
(1)根據已知條件完成下面2×2列聯表,并據此資料你是否認為“體育迷”與性別有關?
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
(2)將上述調查所得到的頻率視為概率.現在從該地區大量電視觀眾中,采用隨機抽樣方法每次抽取1名觀眾,抽取3次,記被抽取的3名觀眾中的“體育迷”人數為X,若每次抽取的結果是相互獨立的,求X的分布列,期望E(X)和方差D(X)
P( K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
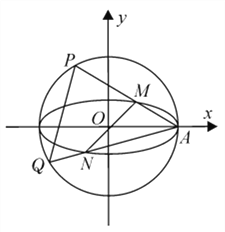
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() ,橢圓
,橢圓![]() ,
, ![]() 為橢圓
為橢圓![]() 的右頂點,過原點且異于
的右頂點,過原點且異于![]() 軸的直線與橢圓
軸的直線與橢圓![]() 交于
交于![]() 兩點,
兩點, ![]() 在
在![]() 軸的上方,直線
軸的上方,直線![]() 與圓
與圓![]() 的另一交點為
的另一交點為![]() ,直線
,直線![]() 與圓
與圓![]() 的另一交點為
的另一交點為![]() ,
,
(1)若![]() ,求直線
,求直線![]() 的斜率;
的斜率;
(2)設![]() 與
與![]() 的面積分別為
的面積分別為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P﹣ABCD中,底面ABCD是一直角梯形,BA⊥AD,AD∥BC,AB=BC=2,PA=3,AD=6,PA⊥底面ABCD,E是PD上的動點.若CE∥平面PAB,則三棱錐C﹣ABE的體積為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知不過第二象限的直線l:ax﹣y﹣4=0與圓x2+(y﹣1)2=5相切.
(1)求直線l的方程;
(2)若直線l1過點(3,﹣1)且與直線l平行,直線l2與直線l1關于直線y=1對稱,求直線l2的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=2cos(ωx+φ)(ω>0,0<φ<π)為奇函數,該函數的部分圖象如圖所示,點A、B分別為該部分圖象的最高點與最低點,且這兩點間的距離為4 ![]() ,則函數f(x)圖象的一條對稱軸的方程為( )
,則函數f(x)圖象的一條對稱軸的方程為( ) 
A.x= ![]()
B.x= ![]()
C.x=4
D.x=2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)的定義域為[﹣1,1],圖象如圖1所示;函數g(x)的定義域為[﹣2,2],圖象如圖2所示,設函數f(g(x))有m個零點,函數g(f(x))有n個零點,則m+n等于( )

A. 6 B. 10 C. 8 D. 1
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com