【題目】在四棱錐P﹣ABCD中，底面ABCD是一直角梯形，BA⊥AD，AD∥BC，AB=BC=2，PA=3，AD=6，PA⊥底面ABCD，E是PD上的動點．若CE∥平面PAB，則三棱錐C﹣ABE的體積為（ ）
A.
B.
C.
D.
【答案】D
【解析】解：以A為原點，AD為x軸，AB為y軸，AP為z軸，建立空間直角坐標系， A（0，0，0），B（0，2，0），C（2，2，0），D（6，0，0），P（0，0，3），
設E（a，0，c）， 
，則（a，0，c﹣3）=（6λ，0，﹣3λ），
解得a=6λ，c=3﹣3λ，∴E（6λ，0，3﹣3λ），
=（6λ﹣2，﹣2，3﹣3λ），
平面ABP的法向量 
=（1，0，0），
∵CE∥平面PAB，∴ 
=6λ﹣2=0，
解得 
，∴E（2，0，2），
∴E到平面ABC的距離d=2，
∴三棱錐C﹣ABE的體積：
VC﹣ABE=VE﹣ABC= 
= 
= 
．
故選：D．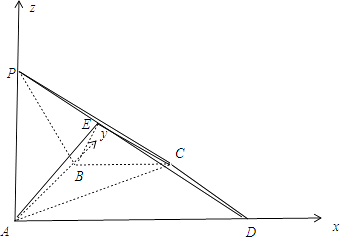
以A為原點，AD為x軸，AB為y軸，AP為z軸，建立空間直角坐標系，利用向量法能求出三棱錐C﹣ABE的體積．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】某公司有4家直營店
， 
， 
， 
，現需將6箱貨物運送至直營店進行銷售，各直營店出售該貨物以往所得利潤統計如下表所示．根據此表，該公司獲得最大總利潤的運送方式有
A. 
種 B. 
種 C. 
種 D. 
種
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若數列
： 
， 
，…， 
（
）中
（
）且對任意的
恒成立，則稱數列
為“
數列”．
（Ⅰ）若數列
， 
， 
， 
為“
數列”，寫出所有可能的
， 
；
（Ⅱ）若“
數列”
： 
， 
，…， 
中， 
， 
，求
的最大值；
（Ⅲ）設
為給定的偶數，對所有可能的“
數列”
： 
， 
，…， 
，
記
，其中
表示
， 
，…， 
這
個數中最大的數，求
的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在古希臘畢達哥拉斯學派把1，3，6，10，15，21，28，…這些數叫做三角形數，因為這些數對應的點可以排成一個正三角形則第n個三角形數為 ．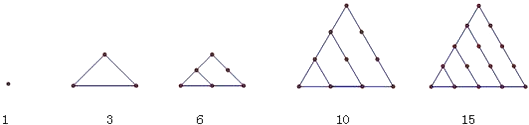 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在幾何體中，四邊形
為菱形，對角線
與
的交點為
，四邊形
為梯形， 
.
（Ⅰ）若
，求證： 
平面
；
（Ⅱ）求證：平面
平面
；
（Ⅲ）若
， 
， 
，求
與平面
所成角.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知Rt△ABC，∠ABC＝90°，D是AC的中點，⊙O經過A，B，D三點，CB的延長線交⊙O于點E，過點E作⊙O的切線，交AC的延長線于點F.在滿足上述條件的情況下，當∠CAB的大小變化時，圖形也隨著改變，但在這個變化過程中，有些線段總保持著相等的關系．
(1)連接圖中已標明字母的某兩點，得到一條新線段與線段CE相等，并說明理由；
(2)若CF＝CD，求sin F的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在△ABC中，角A，B，C所對的邊分別為a，b，c，且滿足2acosC﹣（2b﹣c）=0．
（1）求角A；
（2）若sinC=2sinB，且a= 
，求邊b，c．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量
=（3，﹣4），
=（6，﹣3），
=（5﹣m，﹣3﹣m）．
（Ⅰ）若點A，B，C不能構成三角形，求實數m應滿足的條件；
（Ⅱ）若△ABC為直角三角形，且C為直角，求實數m的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
