
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 作出函數的圖象,先求出f(x)=$\frac{1}{2}$的根,然后利用數形結合轉化為兩個函數的交點個數即可.
解答 解:作出函數f(x)的圖象如圖: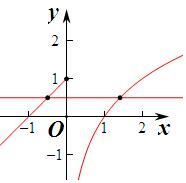
當x≤0時,由f(x)=$\frac{1}{2}$得x+1=$\frac{1}{2}$,即x=$\frac{1}{2}$-1=-$\frac{1}{2}$,
當x>0時,由f(x)=$\frac{1}{2}$得log2x=$\frac{1}{2}$,即x=${2}^{\frac{1}{2}}$=$\sqrt{2}$,
由g(x)=f(f(x))-$\frac{1}{2}$=0得f(f(x))=$\frac{1}{2}$,
則f(x)=-$\frac{1}{2}$或f(x)=$\sqrt{2}$,
若f(x)=-$\frac{1}{2}$,此時方程f(x)=-$\frac{1}{2}$有兩個交點,
若f(x)=$\sqrt{2}$,此時方程f(x)=$\sqrt{2}$只有一個交點,
則數g(x)=f(f(x))-$\frac{1}{2}$的零點個數是3個,
故選:B
點評 本題主要考查函數與方程的應用,利用函數與方程的關系將條件轉化為兩個函數的交點問題是解決本題的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | $±\frac{7}{9}$ | B. | $±\frac{{4\sqrt{2}}}{7}$ | C. | $±2\sqrt{2}$ | D. | $±\frac{{\sqrt{2}}}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
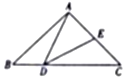 如圖所示,在△ABC中,點D為BC邊上一點,且BD=1,E為AC的中點,AE=$\frac{3}{2}$,cosB=$\frac{{2\sqrt{7}}}{7}$,∠ADB=$\frac{2π}{3}$.
如圖所示,在△ABC中,點D為BC邊上一點,且BD=1,E為AC的中點,AE=$\frac{3}{2}$,cosB=$\frac{{2\sqrt{7}}}{7}$,∠ADB=$\frac{2π}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分而不必要條件 | B. | 必要而不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com