
【題目】為了進一步推動全市學習型黨組織、學習型社會建設,某市組織開展“學習強國”知識測試,每人測試文化、經濟兩個項目,每個項目滿分均為60分.從全體測試人員中隨機抽取了100人,分別統計他們文化、經濟兩個項目的測試成績,得到文化項目測試成績的頻數分布表和經濟項目測試成績的頻率分布直方圖如下:

經濟項目測試成績頻率分布直方圖
分數區間 | 頻數 |
| 2 |
| 3 |
| 5 |
| 15 |
| 40 |
| 35 |
文化項目測試成績頻數分布表
將測試人員的成績劃分為三個等級如下:分數在區間![]() 內為一般,分數在區間
內為一般,分數在區間![]() 內為良好,分數在區間
內為良好,分數在區間![]() 內為優秀.
內為優秀.
(1)在抽取的100人中,經濟項目等級為優秀的測試人員中女生有14人,經濟項目等級為一般或良好的測試人員中女生有34人.填寫下面列聯表,并根據列聯表判斷是否有![]() 以上的把握認為“經濟項目等級為優秀”與性別有關?
以上的把握認為“經濟項目等級為優秀”與性別有關?
優秀 | 一般或良好 | 合計 | |
男生數 | |||
女生數 | |||
合計 |
(2)用這100人的樣本估計總體.
(i)求該市文化項目測試成績中位數的估計值.
(ii)對該市文化項目、經濟項目的學習成績進行評價.
附:
| 0.150 | 0.050 | 0.010 |
| 2.072 | 3.841 | 6.635 |
![]() .
.
【答案】(1)見解析;(2)(i)46.25 (ii)見解析
【解析】
(1)由題意填寫列聯表,計算觀測值,對照臨界值得出結論;
(2)(i)由頻率分布表求得頻率,找到中位數所在的區間,利用比例求解即可;
(ii)評價標準不唯一,可從中位數角度,也可從良好率、優秀率或眾數、平均數角度比較說明均可.
(1)由頻率分布直方圖,得經濟項目等級為優秀人數為![]() .其中女生數為14人,男生數為26人.經濟項目等級為一般或良好的60名測試人員中,女生數為34人,男生數為26人.作出
.其中女生數為14人,男生數為26人.經濟項目等級為一般或良好的60名測試人員中,女生數為34人,男生數為26人.作出![]() 列聯表:
列聯表:
優秀 | 一般或良好 | 合計 | |
男生數 | 26 | 26 | 52 |
女生數 | 14 | 34 | 48 |
合計 | 40 | 60 | 100 |
![]() .
.
由于![]() ,故有
,故有![]() 以上的把握認為“經濟項目等級為優秀”與性別有關.
以上的把握認為“經濟項目等級為優秀”與性別有關.
(2)(i)由頻數分布表知,文化項目測試成績低于40分的頻率為![]() ,測試成績低于50分的頻率為
,測試成績低于50分的頻率為![]() .
.
故該市文化項目測試成績中位數的估計值為![]() .
.
(ii)①由直方圖知,經濟項目測試成績低于40分的頻率為![]() ,測試成績低于50分的頻率為
,測試成績低于50分的頻率為![]() ,故該市文化項目測試成績中位數的估計值為
,故該市文化項目測試成績中位數的估計值為![]() .
.
![]() ,所以該市文化項目學習成績的更好.
,所以該市文化項目學習成績的更好.
②文化項目測試成績良好率估計值為0.9,經濟項目測試成績良好率估計值為0.8,![]() ,所以該市文化項目學習成績的更好.
,所以該市文化項目學習成績的更好.
③文化項目測試成績平均數的估計值為
![]()
![]() .
.
經濟項目測試成績平均數的估計值為
![]()
![]() .
.
因為![]() ,所以該市文化項目學習成績的更好.
,所以該市文化項目學習成績的更好.
④文化項目測試成績優秀率估計值為0.35,經濟項目測試成績優秀率估計值為0.4,![]() ,所以該市對經濟項目學習研究的更深入.
,所以該市對經濟項目學習研究的更深入.
⑤該市文化項目測試成績眾數的估計值為45(分).
經濟項目測試成績眾數的估計值為55(分).
因為![]() ,所以該市對經濟項目學習研究的更深入.
,所以該市對經濟項目學習研究的更深入.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() 平面
平面![]() ,二面角
,二面角![]() 的平面角為
的平面角為![]() ,
,![]() 為
為![]() 中點,
中點,![]() 為
為![]() 中點.
中點.
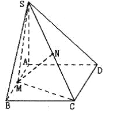
(1)證明:![]() 平面
平面![]() ;
;
(2)證明:平面![]() 平面
平面![]() ;
;
(3)若![]() ,求實數
,求實數![]() 的值,使得直線
的值,使得直線![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】南北朝時代的偉大科學家祖暅在數學上有突出貢獻,他在實踐的基礎上提出祖暅原理:“冪勢既同,則積不容異”. 其含義是:夾在兩個平行平面之間的兩個幾何體,被平行于這兩個平行平面的任意平面所截,如果截得的兩個截面的面積總相等,那么這兩個幾何體的體積相等.如圖,夾在兩個平行平面之間的兩個幾何體的體積分別為![]() ,被平行于這兩個平面的任意平面截得的兩個截面面積分別為
,被平行于這兩個平面的任意平面截得的兩個截面面積分別為![]() ,則“
,則“![]() 相等”是“
相等”是“![]() 總相等”的
總相等”的

A. 充分而不必要條件B. 必要而不充分條件
C. 充分必要條件D. 既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面是邊長為2的正方形,
中,底面是邊長為2的正方形,![]() ⊥底面
⊥底面![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .
.

(1)求證:![]() ;
;
(2)求異面直線![]() 與
與![]() 所成的角的大小(結果用反三角函數表示);
所成的角的大小(結果用反三角函數表示);
(3)若直線![]()
![]() 與平面
與平面![]() 所成角分別為
所成角分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,動點
中,動點![]() 到定點
到定點![]() 的距離與
的距離與![]() 到定直線
到定直線![]() 的距離的比為
的距離的比為![]() ,動點
,動點![]() 的軌跡記為
的軌跡記為![]() .
.
(1)求軌跡![]() 的方程;
的方程;
(2)若點![]() 在軌跡
在軌跡![]() 上運動,點
上運動,點![]() 在圓
在圓![]() 上運動,且總有
上運動,且總有![]() ,
,
求![]() 的取值范圍;
的取值范圍;
(3)過點![]() 的動直線
的動直線![]() 交軌跡
交軌跡![]() 于
于![]() 兩點,試問:在此坐標平面上是否存在一個定點
兩點,試問:在此坐標平面上是否存在一個定點![]() ,使得無論
,使得無論![]() 如何轉動,以
如何轉動,以![]() 為直徑的圓恒過點
為直徑的圓恒過點![]() ?若存在,求出點
?若存在,求出點![]() 的坐標.若不存在,請說明理由.
的坐標.若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型商場去年國慶期間累計生成![]() 萬張購物單,從中隨機抽出
萬張購物單,從中隨機抽出![]() 張,對每單消費金額進行統計得到下表:
張,對每單消費金額進行統計得到下表:
消費金額(單位:元) |
|
|
|
|
|
購物單張數 | 25 | 25 | 30 | 10 | 10 |
由于工作人員失誤,后兩欄數據已無法辨識,但當時記錄表明,根據由以上數據繪制成的頻率分布直方圖所估計出的每單消費額的中位數與平均數恰好相等.用頻率估計概率,完成下列問題:
(1)估計去年國慶期間該商場累計生成的購物單中,單筆消費額超過![]() 元的概率;
元的概率;
(2)為鼓勵顧客消費,該商場打算在今年國慶期間進行促銷活動,凡單筆消費超過![]() 元者,可抽獎一次,中一等獎、二等獎、三等獎的顧客可以分別獲得價值
元者,可抽獎一次,中一等獎、二等獎、三等獎的顧客可以分別獲得價值![]() 元、
元、![]() 元、
元、![]() 元的獎品.已知中獎率為
元的獎品.已知中獎率為![]() ,且一等獎、二等獎、三等獎的中獎率依次構成等比數列,其中一等獎的中獎率為
,且一等獎、二等獎、三等獎的中獎率依次構成等比數列,其中一等獎的中獎率為![]() .若今年國慶期間該商場的購物單數量比去年同期增長
.若今年國慶期間該商場的購物單數量比去年同期增長![]() ,式預測商場今年國慶期間采辦獎品的開銷.
,式預測商場今年國慶期間采辦獎品的開銷.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,短軸端點與兩焦點圍成的三角形面積為
,短軸端點與兩焦點圍成的三角形面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且過點
兩點,且過點![]() ,
,![]() 為坐標原點,當△
為坐標原點,當△![]() 為直角三角形,求直線
為直角三角形,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com