
分析 求出圓心坐標,根據圓關于直線對稱,得到圓心在直線上,得到tanθ=-2,利用1的代換進行求解即可.
解答 解:圓C1:x2+y2+ax=0的圓心坐標為(-$\frac{a}{2}$,0),圓C2:x2+y2+2ax+ytanθ=0的圓心坐標為(-a,-$\frac{tanθ}{2}$),
∵兩圓都關于直線2x-y-1=0對稱,
∴圓心都在方程為2x-y-1=0的直線上,
則-$\frac{a}{2}$×2-1=0,得a=-1,
-2a+$\frac{tanθ}{2}$-1=0,即2+$\frac{tanθ}{2}$-1=0則$\frac{tanθ}{2}$=-1,即tanθ=-2,
則sinθcosθ=$\frac{sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{tanθ}{1+ta{n}^{2}θ}$=-$\frac{2}{5}$,
故答案為-$\frac{2}{5}$.
點評 本題主要考查三角函數值的化簡和計算,根據圓的對稱性,得到a,tanθ的值是解決本題的關鍵.綜合性較強.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $?x∈(1,+∞),x_0^2+2{x_0}+2>0$ | B. | $?x∈({-∞,1}],x_0^2+2{x_0}+2>0$ | ||
| C. | $?{x_0}∈(1,+∞),x_0^2+2{x_0}+2>0$ | D. | $?{x_0}∈({-∞,1}],x_0^2+2{x_0}+2>0$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 15 | B. | $\frac{5}{3}$ | C. | 5 | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{5}$=1(y≠0) | B. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{9}$=1(y≠0) | C. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1(y≠0) | D. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{9}$=1(y≠0) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
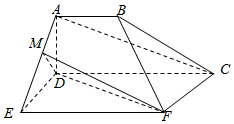 如圖,空間幾何體ADE-BCF中,四邊形ABCD是梯形,四邊形CDEF
如圖,空間幾何體ADE-BCF中,四邊形ABCD是梯形,四邊形CDEF查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 是否愿意提供志愿者服務 性別 | 愿意 | 不愿意 |
| 男生 | 25 | 5 |
| 女生 | 15 | 15 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com