
【題目】已知函數(shù)![]() ,實數(shù)
,實數(shù)![]() 為常數(shù)).
為常數(shù)).
(1)若![]() ,且函數(shù)
,且函數(shù)![]() 在
在![]() 上的最小值為0,求
上的最小值為0,求![]() 的值;
的值;
(2)若對于任意的實數(shù)![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上總是減函數(shù),對每個給定的
上總是減函數(shù),對每個給定的![]() ,求
,求![]() 的最大值
的最大值![]() .
.
【答案】(1)![]() ;(2)
;(2)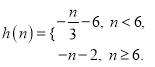 .
.
【解析】試題分析:(1)先求導,求函數(shù)在已知區(qū)間上的極值,注意極值點是否在定義域內(nèi),進行分類討論,確定最小值,列出關于![]() 的方程即可得結果;(2)函數(shù)在區(qū)間上單調(diào)遞減,轉(zhuǎn)化為導函數(shù)小于等于0恒成立,再轉(zhuǎn)化為二次函數(shù)根的分布問題.
的方程即可得結果;(2)函數(shù)在區(qū)間上單調(diào)遞減,轉(zhuǎn)化為導函數(shù)小于等于0恒成立,再轉(zhuǎn)化為二次函數(shù)根的分布問題.
試題解析:(1)當![]() 時,
時, ![]() .
.
則![]() .
.
令![]() ,得
,得![]() (舍),
(舍),![]() .
.
①當![]() >1時,
>1時,
| 1 |
|
|
|
| - | 0 | + | |
|
| ↘ |
| ↗ |
∴當![]() 時,
時, ![]() .
.
令![]() ,得
,得![]() .
.
②當![]() 時,
時, ![]() ≥0在
≥0在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上為增函數(shù),當
上為增函數(shù),當![]() 時,
時, ![]() .
.
令![]() ,得
,得![]() (舍).
(舍).
綜上所述,所求![]() 為
為![]() .
.
(2) ∵對于任意的實數(shù)![]() ,
, ![]() ,
, ![]() 在區(qū)間
在區(qū)間![]() 上總是減函數(shù),
上總是減函數(shù),
則對于x∈(1,3), ![]() <0,
<0,
∴![]() 在區(qū)間[1,3]上恒成立.
在區(qū)間[1,3]上恒成立.
設g(x)= ![]() ,∵
,∵![]() ,∴g(x)
,∴g(x) ![]() 在區(qū)間[1,3]上恒成立.
在區(qū)間[1,3]上恒成立.
由g(x)二次項系數(shù)為正,得
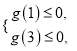 即
即![]() 亦即
亦即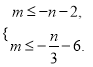
∵![]()
![]() =
=![]() ,
,
∴ 當n<6時,m≤![]() ,當n≥6時,m≤
,當n≥6時,m≤![]() ,
,
∴ 當n<6時,h(n)= ![]() ,當n≥6時,h(n)=
,當n≥6時,h(n)= ![]() ,
,
即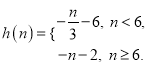


科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() 在
在![]() 上存在零點,求實數(shù)
上存在零點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)當![]() 時, 若對任意的
時, 若對任意的![]() ,總存在
,總存在![]() 使
使![]() 成立, 求實數(shù)
成立, 求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設關于x的一元二次方程x2+2ax+b2=0.
(1)若a是從0,1,2,3四個數(shù)中任取的一個數(shù),b是從0,1,2三個數(shù)中任取的一個數(shù),求上述方程有實根的概率.
(2)若a是從區(qū)間[0,3]任取的一個數(shù),b是從區(qū)間[0,2]任取的一個數(shù),求上述方程有實根的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙兩所學校高三年級分別有1 200人,1 000人,為了了解兩所學校全體高三年級學生在該地區(qū)六校聯(lián)考的數(shù)學成績情況,采用分層抽樣方法從兩所學校一共抽取了110名學生的數(shù)學成績,并作出了頻數(shù)分布統(tǒng)計表如下:
甲校:
分組 | [70,80) | [80,90) | [90,100) | [100,110) |
頻數(shù) | 3 | 4 | 8 | 15 |
分組 | [110,120) | [120,130) | [130,140) | [140,150] |
頻數(shù) | 15 | x | 3 | 2 |
乙校:
分組 | [70,80) | [80,90) | [90,100) | [100,110) |
頻數(shù) | 1 | 2 | 8 | 9 |
分組 | [110,120) | [120,130) | [130,140) | [140,150] |
頻數(shù) | 10 | 10 | y | 3 |
則x,y的值分別為( )
(A)、12,7 (B)、 10,7 (C)、 10,8 (D)、 11,9
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,為測量山高MN,選擇A和另一座山的山頂C為測量觀測點.從A點測得 M點的仰角∠MAN=60°,C點的仰角∠CAB=45°以及∠MAC=75°;從C點測得∠MCA=60°.已知山高BC=100m,則山高MN=m. 
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知命題p:函數(shù) ![]() 在(﹣∞,+∞)上有極值,命題q:雙曲線
在(﹣∞,+∞)上有極值,命題q:雙曲線 ![]() 的離心率e∈(1,2).若p∨q是真命題,p∧q是假命題,求實數(shù)a的取值范圍.
的離心率e∈(1,2).若p∨q是真命題,p∧q是假命題,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知三角形的頂點分別為A(﹣1,3),B(3,2),C(1,0)
(1)求BC邊上高的長度;
(2)若直線l過點C,且在l上不存在到A,B兩點的距離相等的點,求直線l的方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com