
在?ABC中,角A、B、C的對邊分別為a、b、c,且角A、B都是銳角,a=6,b=5,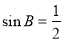 .
.
(1) 求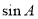 和
和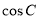 的值;
的值;
(2) 設函數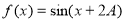 ,求
,求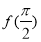 的值.
的值.
(1)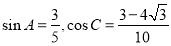 (2)
(2)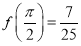
【解析】
試題分析:
(1)在三角形ABC中,可以利用A,B角的正弦定理把A角的正弦值求出來,因為A,B角都是銳角,所以利用正余弦之間的關系可以求出A,B角的余弦值,再根據三角形的三個內角和為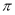 ,可得
,可得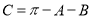 ,則利用誘導公式和余弦的和差角公式即可利用A,B角的正余弦值來表示角C的余弦值.進而求的角c的余弦值.
,則利用誘導公式和余弦的和差角公式即可利用A,B角的正余弦值來表示角C的余弦值.進而求的角c的余弦值.
(2)把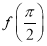 帶入函數
帶入函數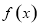 的解析式,利用誘導公式(奇變偶不變,符號看象限)可得
的解析式,利用誘導公式(奇變偶不變,符號看象限)可得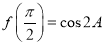 ,利用余弦值的二倍角公式可以利用角A的正弦值或者余弦值來求的
,利用余弦值的二倍角公式可以利用角A的正弦值或者余弦值來求的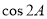 ,進而得到
,進而得到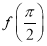 的值.
的值.
試題解析:
(1)由正弦定理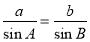 ,得
,得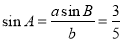 . (3分)
. (3分)
∵A、B是銳角,∴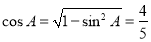 , (4分)
, (4分)
 , (5分)
, (5分)
由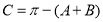 ,得
,得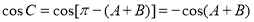 (6分)
(6分)
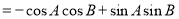 (7分)
(7分)
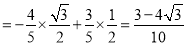 (8分)
(8分)
(2)由(1)知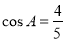 ,
,
∴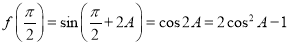 (11分)
(11分)
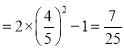 (12分)
(12分)
考點:正余弦值的關系 正余弦值的和差角公式 誘導公式 余弦倍角公式


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源:2013-2014學年廣東省韶關市高三4月高考模擬(二模)文科數學試卷(解析版) 題型:選擇題
在某次測量中得到的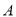 樣本數據如下:82、84、84、86、86、86、88、88、88、88.若
樣本數據如下:82、84、84、86、86、86、88、88、88、88.若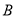 樣本數據恰好是
樣本數據恰好是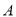 樣本數據每一個數都加2后所得數據,則
樣本數據每一個數都加2后所得數據,則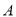 、
、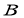 兩個樣本的下列數字特征對應相同的是( )
兩個樣本的下列數字特征對應相同的是( )
A.眾數 B.平均數 C.中位數 D.方差
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省肇慶市高三3月第一次模擬理科數學試卷(解析版) 題型:選擇題
下列命題中,真命題是 ( )
A. ,
,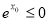 ;
;
B.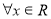 ,
,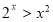 ;
;
C.“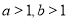 ”是“
”是“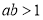 ”的充分不必要條件;
”的充分不必要條件;
D.設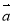 ,
,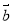 為向量,則“
為向量,則“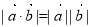 ”是“
”是“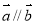 ”的必要不充分條件
”的必要不充分條件
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省肇慶市高三3月第一次模擬文科數學試卷(解析版) 題型:解答題
設函數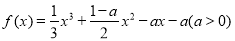 .
.
(1)若函數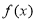 在區間(-2,0)內恰有兩個零點,求a的取值范圍;
在區間(-2,0)內恰有兩個零點,求a的取值范圍;
(2)當a=1時,求函數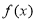 在區間[t,t+3]上的最大值.
在區間[t,t+3]上的最大值.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省湛江市高三高考模擬測試二理科數學試卷(解析版) 題型:選擇題
對于任意兩個正整數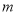 、
、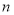 ,定義某種運算“※”,法則如下:當
,定義某種運算“※”,法則如下:當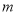 、
、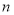 都是正奇數時,
都是正奇數時,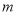 ※
※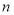 =
=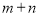 ;當
;當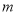 、
、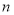 不全為正奇數時,
不全為正奇數時,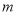 ※
※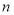 =
=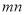 .則在此定義下,集合
.則在此定義下,集合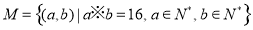 中的元素個數是( )
中的元素個數是( )
A.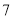 B.
B.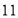 C.
C.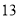 D.
D.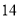
查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東省汕頭市高三3月高考模擬考試文科試卷(解析版) 題型:選擇題
“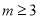 ”是“關于
”是“關于 、
、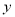 的不等式組
的不等式組 表示的平面區域為三角形”的( )
表示的平面區域為三角形”的( )
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com