
【題目】已知![]() ,記
,記![]() 為正整數a的各位數字之和。試求正整數t的最小值,使得在任意t個連續的正整數中總能找到一個數c,滿足
為正整數a的各位數字之和。試求正整數t的最小值,使得在任意t個連續的正整數中總能找到一個數c,滿足![]() 。
。
【答案】見解析
【解析】
設![]() .則
.則
當10![]() (a+1)時,f(a+1)=f(a)+1;
(a+1)時,f(a+1)=f(a)+1;
當![]() 時,
時,
![]() .
.
首先證明:在任意![]() 個連續正整數中,總能找到一個數c,滿足m|f(c).
個連續正整數中,總能找到一個數c,滿足m|f(c).
若這t個數中有![]() 的倍數,設其為
的倍數,設其為![]() .
.
則f(a)=f(b)=s.
由![]() ,其中,u=0,1,...,8;v=0,1,...,k,知
,其中,u=0,1,...,8;v=0,1,...,k,知![]() 的f值為
的f值為
![]() ,
,
其中,必有一個為9k+r的倍數.
由![]() ,其中,u=0,1,...,9;u=0,1,...,k,知
,其中,u=0,1,...,9;u=0,1,...,k,知![]() 的f值為
的f值為
![]() ,
,
其中,必有一個為9k+r的倍數.
若這t個數中沒有![]() 的倍數,則其中有
的倍數,則其中有![]() 的倍數.設最小的倍數為a,f(a)=s.
的倍數.設最小的倍數為a,f(a)=s.
同上,知![]() 的f值為
的f值為![]() ,其中,必有一個為9k+r的倍數.
,其中,必有一個為9k+r的倍數.
綜上,在![]() 個連續正整數中必有一數c,滿足m|f(c).
個連續正整數中必有一數c,滿足m|f(c).
從而,![]() .
.
其次,分三種情形求![]() .
.
1 當r=1,2,4,5,7,8時,![]() .
.
下面構造![]() 個連續正整數,使得其中沒有數c,滿足mlf(c).
個連續正整數,使得其中沒有數c,滿足mlf(c).
取![]() ,滿足(9k+r)|(9i+1).則在
,滿足(9k+r)|(9i+1).則在![]() 中,只有首尾兩數的f值是9k+r的倍數.故中間的
中,只有首尾兩數的f值是9k+r的倍數.故中間的![]() 個連續正整數中沒有數c,滿足(9k+r)|f(c).
個連續正整數中沒有數c,滿足(9k+r)|f(c).
2 當r=3,6時,![]() .
.
因![]() 個連續正整數中必有一數c,滿足(9k+r)|f(c).此時,3|f(c).而
個連續正整數中必有一數c,滿足(9k+r)|f(c).此時,3|f(c).而![]() 的末尾三數中各自只有一個數是3的倍數,故在連續
的末尾三數中各自只有一個數是3的倍數,故在連續![]() 個數A中首尾共
個數A中首尾共![]() 個數可以去掉,即在
個數可以去掉,即在![]() 個連續正整數中必有一數c,滿足(9h+r)|f(c).
個連續正整數中必有一數c,滿足(9h+r)|f(c).
下面構造![]() 個連續正整數,使得其中沒有數c,滿足m|f(c).
個連續正整數,使得其中沒有數c,滿足m|f(c).
取![]() ,滿足(9k+r)|(9i+3),則在
,滿足(9k+r)|(9i+3),則在![]() 至
至![]() 這
這![]() 個連續正整數中沒有數c,滿足(9k+r)|f(c).
個連續正整數中沒有數c,滿足(9k+r)|f(c).
3 當r=9時,![]() .
.
類似(2)知,9|f(c)且![]() 的末尾九個數中各自只有一個數是9的倍數.
的末尾九個數中各自只有一個數是9的倍數.
故在![]() 個連續正整數中必有一數c,滿足9(k+1)|f(c),且在
個連續正整數中必有一數c,滿足9(k+1)|f(c),且在
![]() 至
至![]() 這
這![]() 個連續正整數中沒有數c,滿足9(k+1)|f(c).
個連續正整數中沒有數c,滿足9(k+1)|f(c).


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】“勾股定理”在西方被稱為“畢達哥拉斯定理”,三國時期吳國的數學家趙爽創制了一幅“勾股圓方圖”,用數形結合的方法給出了勾股定理的詳細證明.如圖所示的“勾股圓方圖”中,四個相同的直角三角形與中間的小正方形拼成一個大正方形,若直角三角形的直角邊的邊長分別是3和4,在繪圖內隨機取一點,則此點取自小正方形的概率為( )
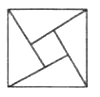
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有9名學生在同一間教室參加一次數學競賽,座位排列成3行3列,用![]() 的方格棋盤表示,其中,每個方格代表一個座位為了避免舞弊,采用A、B、C三種類型的試卷,要使任何兩個相鄰的座位(有公共邊的兩個方格)發放的試卷類型不同.則符合條件的發放試卷的方法共有________種.
的方格棋盤表示,其中,每個方格代表一個座位為了避免舞弊,采用A、B、C三種類型的試卷,要使任何兩個相鄰的座位(有公共邊的兩個方格)發放的試卷類型不同.則符合條件的發放試卷的方法共有________種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在邊長為![]() 的菱形
的菱形![]() 中,
中,![]() .點
.點![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上,點
上,點![]() 與點
與點![]() ,
,![]() 不重合,
不重合,![]() ,
,![]() .沿
.沿![]() 將
將![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(1)求證:![]() 平面
平面![]() ;
;
(2)當![]() 與平面
與平面![]() 所成的角為
所成的角為![]() 時,求平面
時,求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 的參數方程為
的參數方程為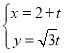 (
(![]() 為參數),
為參數),![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程及曲線
的普通方程及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,設
兩點,設![]() 、
、![]() 中點為
中點為![]() ,求弦長
,求弦長![]() 以及
以及![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌經銷商在一廣場隨機采訪男性和女性用戶各50名,其中每天玩微信超過6小時的用戶列為“微信控”,否則稱其為“非微信控”,調查結果如下:
微信控 | 非微信控 | 合計 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合計 | 56 | 44 | 100 |
(1)根據以上數據,能否有95%的把握認為“微信控”與“性別”有關?
(2)現從調查的女性用戶中按分層抽樣的方法選出5人,再隨機抽取3人贈送禮品,記這3人中“微信控”的人數為![]() ,試求
,試求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式:  ,其中
,其中![]() .
.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com