
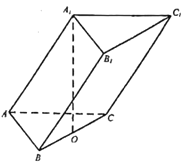
【題目】在三棱柱![]() 中,
中,![]() 是正三角形,
是正三角形,![]() ,點
,點![]() 在底面
在底面![]() 上的射影
上的射影![]() 恰好是
恰好是![]() 中點,側棱和底面成
中點,側棱和底面成![]() 角.
角.
(1)求證:![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直線![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
【答案】(1)證明見解析;(2)二面角![]() 的大小為
的大小為![]() .
.
(3)直線![]() 與平面
與平面![]() 所成角為
所成角為![]()
【解析】
(1)先證明![]() 平面
平面![]() ,根據線面垂直的定義即可得結論;
,根據線面垂直的定義即可得結論;
(2)建立空間直角坐標系,分別求出平面![]() ,平面
,平面![]() 的法向量,求出兩法向量的夾角,結合圖形即可求解;
的法向量,求出兩法向量的夾角,結合圖形即可求解;
(3)根據(2)求出的平面![]() 的法向量,結合直線
的法向量,結合直線![]() 的方向向量,即可求解.
的方向向量,即可求解.
(1)連接![]() ,因為
,因為![]() 為
為![]() 的中點,
的中點,![]() 為正三角形,所以
為正三角形,所以![]() ,由點
,由點![]() 在底面
在底面![]() 上的射影為
上的射影為![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 所以
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)以![]() 為原點,
為原點,![]() 分別為
分別為![]() 軸建立空間直角坐標系如圖.
軸建立空間直角坐標系如圖. 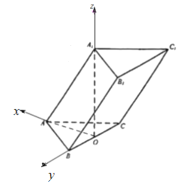 則
則![]() 因為側棱和底面成
因為側棱和底面成![]() 角,所以
角,所以![]() ,則
,則![]() ,設平面
,設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則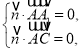 即
即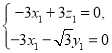 令
令![]() ,則
,則![]() .設平面
.設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則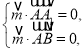 即
即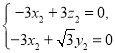 令
令![]() ,則
,則![]() .所以
.所以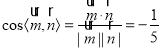 ,由圖可知二面角
,由圖可知二面角![]() 為銳角,所以二面角
為銳角,所以二面角![]() 的大小為
的大小為![]() .
.
(3)由(2)可知平面![]() 的法向量為
的法向量為![]() ,設直線
,設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,所以
,所以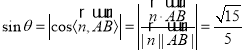 ,所以直線
,所以直線![]() 與平面
與平面![]() 所成角為
所成角為![]()


科目:高中數學 來源: 題型:
【題目】某中學在高二下學期開設四門數學選修課,分別為《數學史選講》.《球面上的幾何》.《對稱與群》.《矩陣與變換》.現有甲.乙.丙.丁四位同學從這四門選修課程中選修一門,且這四位同學選修的課程互不相同,下面關于他們選課的一些信息:①甲同學和丙同學均不選《球面上的幾何》,也不選《對稱與群》:②乙同學不選《對稱與群》,也不選《數學史選講》:③如果甲同學不選《數學史選講》,那么丁同學就不選《對稱與群》.若這些信息都是正確的,則丙同學選修的課程是( )
A. 《數學史選講》B. 《球面上的幾何》C. 《對稱與群》D. 《矩陣與變換》
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖象上所有點的縱坐標伸長到原來的
的圖象上所有點的縱坐標伸長到原來的![]() 倍(橫坐標不變),再向左平移
倍(橫坐標不變),再向左平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象,設函數
的圖象,設函數![]() .
.
(1)對函數![]() 的解析式;
的解析式;
(2)若對任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(3)若![]() 在
在![]() 內有兩個不同的解
內有兩個不同的解![]() ,
,![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個不相等的非零向量![]() 與
與![]() ,兩組向量
,兩組向量![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 和
和![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均有2個
均有2個![]() 和3個
和3個![]() 按照某種順序排成一列所構成,記
按照某種順序排成一列所構成,記![]()
![]() ,且
,且![]() 表示
表示![]() 所有可能取值中的最小值,有以下結論:①有5個不同的值;②若
所有可能取值中的最小值,有以下結論:①有5個不同的值;②若![]() ,則
,則![]() 與
與![]() 無關;③ 若
無關;③ 若![]() ∥
∥![]() ,則
,則![]() 與
與![]() 無關;④ 若
無關;④ 若![]() ,則
,則![]() ;⑤若
;⑤若![]() ,且
,且![]() ,則
,則![]() 與
與![]() 的夾角為
的夾角為![]() ;正確的結論的序號是( )
;正確的結論的序號是( )
A.①②④B.②④C.②③D.①⑤
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了測量某塔的高度,某人在一條水平公路![]() 兩點進行測量.在
兩點進行測量.在![]() 點測得塔底
點測得塔底![]() 在南偏西
在南偏西![]() ,塔頂仰角為
,塔頂仰角為![]() ,此人沿著南偏東
,此人沿著南偏東![]() 方向前進10米到
方向前進10米到![]() 點,測得塔頂的仰角為
點,測得塔頂的仰角為![]() ,則塔的高度為( )
,則塔的高度為( )
A. 5米B. 10米C. 15米D. 20米
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出以下命題,
①命題“若![]() ,則
,則![]() 或
或![]() ”為真命題;
”為真命題;
②命題“若![]() ,則
,則![]() ”的否命題為真命題;
”的否命題為真命題;
③若平面![]() 上不共線的三個點到平面
上不共線的三個點到平面![]() 距離相等,則
距離相等,則![]()
④若![]() ,
,![]() 是兩個不重合的平面,直線
是兩個不重合的平面,直線![]() ,命題
,命題![]() ,命題
,命題![]() ,則
,則![]() 是
是![]() 的必要不充分條件;
的必要不充分條件;
⑤平面![]() 過正方體
過正方體![]() 的三個頂點
的三個頂點![]() ,且
,且![]() 與底面
與底面![]() 的交線為
的交線為![]() ,則
,則![]() ∥
∥![]() ;
;
其中,真命題的序號是______
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com