
已知:sinβ=![]() ,sin(α+β)=1.求sin(2α+β)的值.
,sin(α+β)=1.求sin(2α+β)的值.
 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案科目:高中數學 來源:2011屆高考數學第一輪復習測試題6 題型:044
(理)已知向量m=(sinωx+cosωx,![]() cosωx),n=(cosωx-sinωx,2 sinωx),其中ω>0,函數f(x)=m·n,若f(x)相鄰兩對稱軸間的距離為
cosωx),n=(cosωx-sinωx,2 sinωx),其中ω>0,函數f(x)=m·n,若f(x)相鄰兩對稱軸間的距離為![]() .
.
(1)求ω的值,并求f(x)的最大值及相應x的集合;
(2)在△ABC中,a、b、c分別是A、B、C所對的邊,△ABC的面積S=5![]() ,b=4,f(A)=1,求邊a的長.
,b=4,f(A)=1,求邊a的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
已知橢圓C:![]() +
+![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為![]() ,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的中點。
,過右焦點F且斜率為1的直線交橢圓C于A,B兩點,N為弦AB的中點。
(1)求直線ON(O為坐標原點)的斜率KON ;
(2)對于橢圓C上任意一點M ,試證:總存在角![]() (
(![]() ∈R)使等式:
∈R)使等式:![]() =cos
=cos![]()
![]() +sin
+sin![]()
![]() 成立。w.w.w.k.s.5.u.c.o.m
成立。w.w.w.k.s.5.u.c.o.m
查看答案和解析>>
科目:高中數學 來源: 題型:
已知角A、B、C為△ABC的三個內角,其對邊分別為a、b、c,若=(-cos,sin),=(cos,sin),a=2,且·=.
(Ⅰ)若△ABC的面積S=,求b+c的值.(Ⅱ)求b+c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
在△![]() 中,已知
中,已知![]() ·
·![]() =9,sin
=9,sin![]() =cos
=cos![]() sin
sin![]() ,面積S
,面積S![]() =6.
=6.
(Ⅰ)求△![]() 的三邊的長;
的三邊的長;
(Ⅱ)設![]() 是△
是△![]() (含邊界)內一點,
(含邊界)內一點,![]() 到三邊
到三邊![]() ,
,![]() ,
,![]() 的距離分別為x,y和z,求x+y+z的取值范圍.
的距離分別為x,y和z,求x+y+z的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010年高考試題(遼寧卷)解析版(文) 題型:解答題
已知函數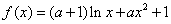 .
.
(Ⅰ)討論函數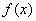 的單調性;
的單調性;
(Ⅱ)設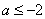 ,證明:對任意
,證明:對任意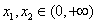 ,
,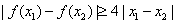 .
.
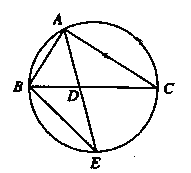 1.選修4-1:幾何證明選講
1.選修4-1:幾何證明選講
如圖, 的角平分線
的角平分線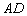 的延長線交它的外接圓于點
的延長線交它的外接圓于點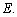
(Ⅰ)證明: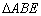 ∽△
∽△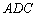 ;
;
(Ⅱ)若 的面積
的面積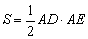 ,求
,求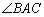 的大小.
的大小.
證明:(Ⅰ)由已知條件,可得∠BAE=∠CAD.
因為∠AEB與∠ACB是同弧上的圓周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因為△ABE∽△ADC,所以 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S= AB·ACsin∠BAC,且S=
AB·ACsin∠BAC,且S= AD·AE,故AB·ACsin∠BAC=AD·AE.
AD·AE,故AB·ACsin∠BAC=AD·AE.
則sin∠BAC=1,又∠BAC為三角形內角,所以∠BAC=90°.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com