
【題目】已知函數![]()
(1)判斷函數![]() 在
在![]() 上的單調性
上的單調性
(2)若![]() 恒成立,求整數
恒成立,求整數![]() 的最大值
的最大值
(3)求證:![]()
科目:高中數學 來源: 題型:
【題目】如圖(1)是某水上樂園擬開發水滑梯項目的效果圖,考慮到空間和安全方面的原因,初步設計方案如下:如圖(2),自直立于水面的空中平臺![]() 的上端點P處分別向水池內的三個不同方向建水滑道
的上端點P處分別向水池內的三個不同方向建水滑道![]() ,
,![]() ,
,![]() ,水滑道的下端點
,水滑道的下端點![]() 在同一條直線上,
在同一條直線上,![]() ,
,![]() 平分
平分![]() ,假設水滑梯的滑道可以看成線段,
,假設水滑梯的滑道可以看成線段,![]() 均在過C且與
均在過C且與![]() 垂直的平面內,為了滑梯的安全性,設計要求
垂直的平面內,為了滑梯的安全性,設計要求![]() .
.
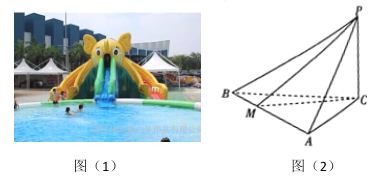
(1)求滑梯的高![]() 的最大值;
的最大值;
(2)現在開發商考慮把該水滑梯項目設計成室內游玩項目,且為保證該項目的趣味性,設計![]() ,求該滑梯裝置(即圖(2)中的幾何體)的體積最小值.
,求該滑梯裝置(即圖(2)中的幾何體)的體積最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是我國2008年至2014年生活垃圾無害化處理量(單位:億噸)的折線圖.

(Ⅰ)由折線圖看出,可用線性回歸模型擬合y與t的關系,請用相關系數加以說明;
(Ⅱ)建立y關于t的回歸方程(系數精確到0.01),預測2016年我國生活垃圾無害化處理量.
附注:
參考數據:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
參考公式:相關系數
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設定義在R上的函數![]() ,當
,當![]() 時,
時,![]() 取極大值
取極大值![]() ,且函數
,且函數![]() 的圖象關于原點對稱.
的圖象關于原點對稱.
(1)求![]() 的表達式;
的表達式;
(2)試在函數![]() 的圖象上求兩點,使以這兩點為切點的切線互相垂直,且切點的橫坐標都在
的圖象上求兩點,使以這兩點為切點的切線互相垂直,且切點的橫坐標都在![]() 上;
上;
(3)設![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場舉行有獎促銷活動,顧客購買一定金額商品后即可抽獎,每次抽獎都從裝有4個紅球、6個白球的甲箱和裝有5個紅球、5個白球的乙箱中,各隨機摸出1個球,在摸出的2個球中,若都是紅球,則獲一等獎;若只有1個紅球,則獲二等獎;若沒有紅球,則不獲獎.
(1)求顧客抽獎1次能獲獎的概率;
(2)若某顧客有3次抽獎機會,記該顧客在3次抽獎中獲一等獎的次數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平而直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]()
(1)求曲線![]() 和
和![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 是曲線
是曲線![]() 上一點、
上一點、![]() 分別是
分別是![]() 和
和![]() 上的點,求
上的點,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com