
若非零函數 對任意實數
對任意實數 均有
均有 ,且當
,且當 時
時
(1)求證: ;
;
(2)求證: 為R上的減函數;
為R上的減函數;
(3)當 時, 對
時, 對 恒有
恒有 ,求實數
,求實數 的取值范圍.
的取值范圍.
(1)證法一: 即
即 又
又 [來源:學&科&網]
[來源:學&科&網]
當 時,
時,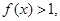

 則
則
故對于 恒有
恒有
證法二:
 為非零函數
為非零函數 
(2)證明:令 且
且
有 , 又
, 又 即
即
故 又
又

故 為R上的減函數
為R上的減函數
(3)實數 的取值范圍為
的取值范圍為
解析試題分析:(1)由題意可取 代入等式
代入等式 ,得出關于
,得出關于 的方程,因為
的方程,因為 為非零函數,故
為非零函數,故 ,再令
,再令 代入等式,可證
代入等式,可證 ,從而證明當
,從而證明當 時,有
時,有 ;(2)著眼于減函數的定義,利用條件當
;(2)著眼于減函數的定義,利用條件當 時,有
時,有 ,根據等式
,根據等式 ,令
,令 ,
, ,可得
,可得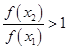 ,從而可證該函數為減函數.(3)根據
,從而可證該函數為減函數.(3)根據 ,由條件
,由條件 可求得
可求得 ,將
,將 替換不等式中的
替換不等式中的 ,再根據函數的單調性可得
,再根據函數的單調性可得 ,結合
,結合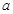 的范圍,從而得解.
的范圍,從而得解.
試題解析:(1)證法一: 即
即 又
又

當 時,
時,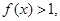

 則
則
故對于 恒有
恒有 4分
4分
證法二:
 為非零函數
為非零函數 
(2)令 且
且
有 , 又
, 又 即
即
故 又
又

故 為R上的減函數 8分
為R上的減函數 8分
(3) 故
故 , 10分
, 10分
則原不等式可變形為
依題意有  對
對 恒成立
恒成立 或
或 或
或
故實數 的取值范圍為
的取值范圍為 14分
14分
考點:1.函數的概念;2.函數的單調性;3.二次函數.


科目:高中數學 來源: 題型:解答題
湖南省環保研究所對長沙市中心每天環境放射性污染情況進行調查研究后,發現一天中環境綜合放射性污染指數 與時刻x的關系為
與時刻x的關系為 ,其中a是與氣象有關的參數,且
,其中a是與氣象有關的參數,且 ,若用每天
,若用每天 的最大值作為當天的綜合放射性污染指數,并記作
的最大值作為當天的綜合放射性污染指數,并記作 .
.
(Ⅰ)令 ,求t的取值范圍;
,求t的取值范圍;
(Ⅱ)省政府規定,每天的綜合放射性污染指數不得超過2,試問目前市中心的綜合放射性污染指數是否超標?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知二次函數 的最小值為
的最小值為 ,且關于
,且關于 的一元二次不等式
的一元二次不等式 的解集為
的解集為 。
。
(Ⅰ)求函數 的解析式;
的解析式;
(Ⅱ)設 其中
其中 ,求函數
,求函數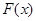 在
在 時的最大值
時的最大值 ;
;
(Ⅲ)若 (
( 為實數),對任意
為實數),對任意 ,總存在
,總存在 使得
使得 成立,求實數
成立,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com