【題目】已知橢圓
過點
, 離心率為
,左右焦點分別為
, 過點
的直線
交橢圓于
兩點.
（1）求橢圓C的方程；
（2）當
的面積為
時, 求以
為圓心且與直線相切的圓的方程.
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ax2+2x+c，若不等式f（x）<0的解集是{x|-4<x<2}.
（1）求f（x）的解析式；
（2）判斷f（x）在（0，+∞）上的單調性，并用定義證明；
（3）若函數f（x）在區間[m，m+2]上的最小值為-5，求實數m的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】科學研究表明：人類對聲音有不的感覺，這與聲音的強度
單位：瓦
平方米
有關
在實際測量時，常用
單位：分貝來表示聲音強弱的等級，它與聲音的強度I滿足關系式：
是常數，其中
瓦平方米如風吹落葉沙沙聲的強度
瓦平方米，它的強弱等級
分貝．
已知生活中幾種聲音的強度如表：
聲音來源
聲音大小 | 風吹落葉沙沙聲 | 輕聲耳語 | 很嘈雜的馬路 |
強度 |
|
|
|
強弱等級 | 10 | m | 90 |
求a和m的值
為了不影響正常的休息和睡眠，聲音的強弱等級一般不能超過50分貝，求此時聲音強度I的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點
，
是函數
（
，
）圖象上的任意兩點，且角
的終邊經過點
，若
時，
的最小值為
．
（1）求函數
的解析式；
（2）當
時，不等式
恒成立，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】類比平面幾何中的定理：△ABC中，若DE是△ABC的中位線，則有S△ADE∶S△ABC＝1∶4；若三棱錐A－BCD有中截面EFG∥平面BCD，則截得三棱錐的體積與原三棱錐體積之間的關系式為________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
的定義域為區間
，若對于內任意
，都有
成立，則稱函數
是區間的“
函數”.
（1）判斷函數
（
）是否是“函數”？說明理由；
（2）已知
，求證：函數
（
）是“函數”；
（3）設函數
是
,（
）上的“函數”，
，且存在
使得
，試探討函數在區間上零點個數，并用圖象作出簡要的說明（結果不需要證明）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠共有男女員工500人，現從中抽取100位員工對他們每月完成合格產品的件數統計如下：
每月完成合格產品的件數（單位：百件） |
|
|
|
|
|
頻數 | 10 | 45 | 35 | 6 | 4 |
男員工人數 | 7 | 23 | 18 | 1 | 1 |
（1）其中每月完成合格產品的件數不少于3200件的員工被評為“生產能手”.由以上統計數據填寫下面
列聯表，并判斷是否有95%的把握認為“生產能手”與性別有關？
非“生產能手” | “生產能手” | 合計 | |
男員工 | |||
女員工 | |||
合計 |
（2）為提高員工勞動的積極性，工廠實行累進計件工資制：規定每月完成合格產品的件數在定額2600件以內的，計件單價為1元；超出
件的部分，累進計件單價為1.2元；超出
件的部分，累進計件單價為1.3元；超出400件以上的部分，累進計件單價為1.4元.將這4段中各段的頻率視為相應的概率，在該廠男員工中選取1人，女員工中隨機選取2人進行工資調查，設實得計件工資（實得計件工資=定額計件工資+超定額計件工資）不少于3100元的人數為，求的分布列和數學期望.
附：
，
.
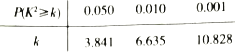查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
