解:(1)設拋物線C
2:y
2=2px(p≠0),則有
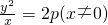
,
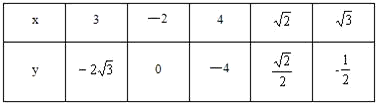
據此驗證5個點知只有(3,
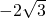
)、(4,-4)在統一拋物線上,易求C
2:y
2=4x
設

,把點(-2,0)(

,

)代入得
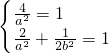
解得

∴C
2方程為

(2)假設存在這樣的直線l過拋物線焦點F(1,0)
設其方程為x-1=my,設M(x
1,y
1),N(x
2,y
2),
由

.得x
1x
2+y
1y
2=0(*)
由
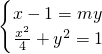
消去x,得(m
2+4)y
2+2my-3=0,△=16m
2+48>0
∴
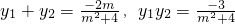
①
x
1x
2=(1+my
1)(1+my
2)=1+m(y
1+y
2)+m
2y
1y
2;
=
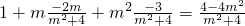
②
將①②代入(*)式,得
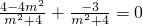
解得
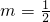
,
∴假設成立,即存在直線l過拋物線焦點Fl的方程為:2x±y-2=0
分析:(1)設拋物線C
2:y
2=2px(p≠0),由題意知C
2:y
2=4x(2分).設

,把點(-2,0)(

,

)代入得
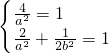
解得

,由此可知C
2的方程.
(2)假設存在這樣的直線l過拋物線焦點F(1,0),設其方程為x-1=my,設M(x
1,y
1),N(x
2,y
2),由

.得x
1x
2+y
1y
2=0.由
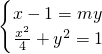
消去x,得(m
2+4)y
2+2my-3=0,然后由根的判別式和根與系數的關系可知假設成立,即存在直線l過拋物線焦點Fl的方程為:2x±y-2=0.
點評:本題考查直線和圓錐曲線的位置關系,解題時要認真審題,仔細解答.

 ,請問是否存在這樣的直線l過拋物線C2的焦點F?若存在,求出直線l的方程;若不存在,說明理由.
,請問是否存在這樣的直線l過拋物線C2的焦點F?若存在,求出直線l的方程;若不存在,說明理由.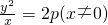 ,
,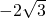 )、(4,-4)在統一拋物線上,易求C2:y2=4x
)、(4,-4)在統一拋物線上,易求C2:y2=4x ,把點(-2,0)(
,把點(-2,0)( ,
, )代入得
)代入得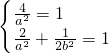 解得
解得

 .得x1x2+y1y2=0(*)
.得x1x2+y1y2=0(*)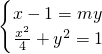 消去x,得(m2+4)y2+2my-3=0,△=16m2+48>0
消去x,得(m2+4)y2+2my-3=0,△=16m2+48>0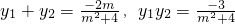 ①
①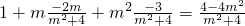 ②
②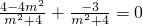
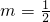 ,
, ,把點(-2,0)(
,把點(-2,0)( ,
, )代入得
)代入得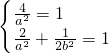 解得
解得 ,由此可知C2的方程.
,由此可知C2的方程. .得x1x2+y1y2=0.由
.得x1x2+y1y2=0.由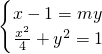 消去x,得(m2+4)y2+2my-3=0,然后由根的判別式和根與系數的關系可知假設成立,即存在直線l過拋物線焦點Fl的方程為:2x±y-2=0.
消去x,得(m2+4)y2+2my-3=0,然后由根的判別式和根與系數的關系可知假設成立,即存在直線l過拋物線焦點Fl的方程為:2x±y-2=0.

 走進文言文系列答案
走進文言文系列答案 (2005•海淀區二模)設橢圓C1的中心在原點,其右焦點與拋物線C2:y2=4x的焦點F重合,過點F與x軸垂直的直線與C1交于A、B兩點,與C2交于C、D兩點,已知
(2005•海淀區二模)設橢圓C1的中心在原點,其右焦點與拋物線C2:y2=4x的焦點F重合,過點F與x軸垂直的直線與C1交于A、B兩點,與C2交于C、D兩點,已知