【題目】已知函數
，其中
（1）若
是
的極值點，求
的值；
（2）求函數的單調區間和極值.
【答案】（1）
；（2）見解析
【解析】
（1）求出函數的導數，根據f′（1）=0，求出m的值即可；（2）求出函數的導數，通過討論m的范圍，得到函數的單調區間，從而判斷函數的極值即可．
（1）f′（x）=4m2x+4m﹣
，
若x=1是f（x）的極值點，
則f′（1）=4m2+4m﹣3=0，
解得：m=﹣
或m=
；
（2）函數f（x）的定義域是（0，+∞），
f′（x）=
，
當m＞0時，令f′（x）＞0，解得：x＞
，
令f′（x）＜0，解得：0＜x＜，
故f（x）在（0，）遞減，在（，+∞）遞增，
f（x）的極小值為f（）=
+3ln（2m）；無極大值．
當m＜0時，令f′（x）＞0，解得：x＞﹣
，
令f′（x）＜0，解得：0＜x＜﹣，
故f（x）在（0，﹣）遞減，在（﹣，+∞）遞增，
故f（x）的極小值為f（﹣）=﹣
﹣3ln（﹣）；無極大值．
當m=0時，f′（x）＜0，減區間為（0，+∞），無增區間和極值．
科目：高中數學 來源： 題型：
【題目】如圖，網格紙上小正方形的邊長為1，粗線畫出的是一正方體被截去一部分后所得幾何體的三視圖，則該幾何體的表面積為（ ）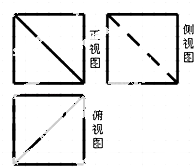 
A.54
B.162
C.54+18 
D.162+18
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知方向向量為v=（1， 
）的直線l過點（0，﹣2 ）和橢圓C： 
=1（a＞b＞0）的焦點，且橢圓C的中心關于直線l的對稱點在橢圓C的右準線上．
（Ⅰ）求橢圓C的方程；
（Ⅱ）是否存在過點E（﹣2，0）的直線m交橢圓C于點M、N，滿足 
= 
．cot∠MON≠0（O為原點）．若存在，求直線m的方程；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設A1 ， A2 ， A3 ， …，An是集合{1，2，3，…，n}的n個非空子集（n≥2），定義aij= 
，其中i，j=1，2，…，n，這樣得到的n2個數之和記為S（A1 ， A2 ， A3 ， …，An），簡記為S，下列三種說法：①S與n的奇偶性相同；②S是n的倍數；③S的最小值為n，最大值為n2 ． 其中正確的判斷是（ ）
A.①②
B.①③
C.②③
D.③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地區為下崗人員免費提供財會和計算機培訓，以提高下崗人員的再就業能力．每名下崗人員可以選擇參加一項培訓、參加兩項培訓或不參加培訓．已知參加過財會培訓的有60%，參加過計算機培訓的有75%，假設每個人對培訓項目的選擇是相互獨立的，且各人的選擇相互之間沒有影響．
（1）任選1名下崗人員，求該人參加過培訓的概率；
（2）任選3名下崗人員，記ξ為3人中參加過培訓的人數，求ξ的分布列．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題共l2分）
如圖，在直三棱柱ABC－A1B1C1中，∠BAC=90°，AB=AC=AA1=1，延長A1C1至點P，使C1P＝A1C1，連接AP交棱CC1于D．
（Ⅰ）求證：PB1∥平面BDA1；
（Ⅱ）求二面角A－A1D－B的平面角的余弦值；
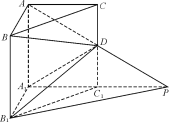
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數
給出定義：
設
是函數
的導數，
是函數的導數，若方程
有實數解
，則稱點
為函數的“拐點”，
某同學經過探究發現：任何一個三次函數
都有“拐點”：任意一個三次函數都有對稱中心，且“拐點”就是對稱中心，給定函數
，請根據上面探究結果：計算
____________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=2sinωxcosωx+2 
sin2ωx﹣ （ω＞0）的最小正周期為π．
（1）求函數f（x）的單調增區間；
（2）將函數f（x）的圖象向左平移 
個單位長度，再向上平移1個單位長度，得到函數y=g（x）的圖象，求函數y=g（x）在 
上的最值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
