
分析 依題意,作圖如下:A(-a,0),B(0,b),F(xiàn)1(-c,0),F(xiàn)2(c,0),直線AB的方程為:bx-ay+ab=0,設(shè)直線AB上的點(diǎn)P(x,y),則bx=ay-ab,由PF1⊥PF2,$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=x2+y2-c2=$(\frac{a}{b}y-a)^{2}$+y2-c2=f(y),令f′(y)=2$\frac{a}{b}$$(\frac{a}{b}y-a)$+2y=0,解得:y=$\frac{{a}^{2}b}{{a}^{2}+{b}^{2}}$,x=-$\frac{a{b}^{2}}{{a}^{2}+{b}^{2}}$,滿足$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,解得e=$\frac{\sqrt{5}-1}{2}$,為最小值.當(dāng)點(diǎn)P取B時,b=c,e=$\frac{\sqrt{2}}{2}$取得最大值.即可得出.
解答 解:依題意,作圖如下: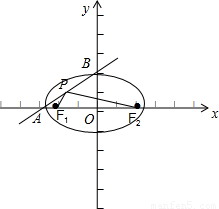
∵A(-a,0),B(0,b),F(xiàn)1(-c,0),F(xiàn)2(c,0),
∴直線AB的方程為:$\frac{x}{-a}$+$\frac{y}{b}$=1.整理得:bx-ay+ab=0,
設(shè)直線AB上的點(diǎn)P(x,y)
則bx=ay-ab,
∴x=$\frac{a}{b}$y-a,
∵PF1⊥PF2,
∴$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=(-c-x,-y)•(c-x,-y)=x2+y2-c2
=$(\frac{a}{b}y-a)^{2}$+y2-c2=f(y),
令f′(y)=2$\frac{a}{b}$$(\frac{a}{b}y-a)$+2y=0,
∴由f′(y)=0得:y=$\frac{{a}^{2}b}{{a}^{2}+{b}^{2}}$,于是x=-$\frac{a{b}^{2}}{{a}^{2}+{b}^{2}}$,
∴$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=$(-\frac{a{b}^{2}}{{a}^{2}+{b}^{2}})^{2}+(\frac{{a}^{2}b}{{a}^{2}+{b}^{2}})^{2}$-c2=0,
整理可得:$\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}$=c2,又b2=a2-c2,e2=$\frac{{c}^{2}}{{a}^{2}}$,
∴e4-3e2+1=0,
∴e2=$\frac{3-\sqrt{5}}{2}$,又橢圓的離心率e∈(0,1),
∴e=$\frac{\sqrt{5}-1}{2}$,為最小值.
當(dāng)點(diǎn)P取B時,b=c,e=$\frac{\sqrt{2}}{2}$.
∴橢圓的離心率的取值范圍為$[\frac{\sqrt{5}-1}{2},\frac{\sqrt{2}}{2}]$.
故答案為:$[\frac{\sqrt{5}-1}{2},\frac{\sqrt{2}}{2}]$.
點(diǎn)評 本題考查了橢圓的標(biāo)準(zhǔn)方程及其性質(zhì)、利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性、數(shù)量積運(yùn)算性質(zhì),考查了推理能力與計(jì)算能力,屬于難題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1 | B. | 4 | C. | -4 | D. | 5 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
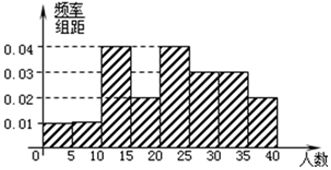
| A. | 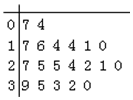 | B. | 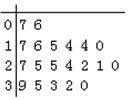 | C. |  | D. |  |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com