
【題目】如圖,在平面直角坐標系中,銳角![]() 和鈍角
和鈍角![]() 的終邊分別與單位圓交于
的終邊分別與單位圓交于![]() 兩點.
兩點.
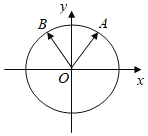
(Ⅰ)如果點![]() 縱坐標分別為
縱坐標分別為![]() ,求
,求![]() ;
;
(Ⅱ)若![]() 為
為![]() 軸上異于
軸上異于![]() 的點,且
的點,且![]() ,求點
,求點![]() 橫坐標的取值范圍.
橫坐標的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)利用三角函數的定義,結合兩角和差的余弦公式進行計算即可;(Ⅱ) 若![]() ,則
,則![]() ,設
,設![]() ,可得
,可得![]() ,利用向量垂直的坐標公式,可得
,利用向量垂直的坐標公式,可得![]() ,由
,由![]() ,結合余弦函數的單調性可得結果.
,結合余弦函數的單調性可得結果.
(Ⅰ)∵點A、B縱坐標分別為![]() 、
、![]() ,
,
∴sinα=![]() ,sinβ=
,sinβ=![]() ,
,
∵α為銳角,β為鈍角,
![]()
![]()
(Ⅱ)依題意得A(cosα,sinα),B(cosβ,sinβ),
∵AOB=90,即β=α+90,
∴B(-sinα,cosα),
設![]()
∴(-x+cosα)(-x-sinα)+sinα·cosα=0,
整理得x2+x(sinα-cosα)=0,(x0),
∴x=cosα-sinα=![]() cos(α+
cos(α+![]() ),(x0),
),(x0),
![]()
所以x(-1,0)∪(0,1).


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:
【題目】雙曲線 ![]() 的左、右焦點分別為F1、F2,直線l過F2且與雙曲線交于A、B兩點.
的左、右焦點分別為F1、F2,直線l過F2且與雙曲線交于A、B兩點.
(1)若l的傾斜角為 ![]() ,
, ![]() 是等邊三角形,求雙曲線的漸近線方程;
是等邊三角形,求雙曲線的漸近線方程;
(2)設 ![]() ,若l的斜率存在,且|AB|=4,求l的斜率.
,若l的斜率存在,且|AB|=4,求l的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的中心在坐標原點,焦點在
的中心在坐標原點,焦點在![]() 軸上,離心率
軸上,離心率![]() ,虛軸長為2.
,虛軸長為2.
(1)求雙曲線![]() 的標準方程;
的標準方程;
(2)若直線![]() 與雙曲線
與雙曲線![]() 相交于
相交于![]() 兩點,(
兩點,( ![]() 均異于左、右頂點),且以
均異于左、右頂點),且以![]() 為直徑的圓過雙曲線
為直徑的圓過雙曲線![]() 的左頂點
的左頂點![]() ,求證:直線
,求證:直線![]() 過定點,并求出該定點的坐標.
過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十九大指出中國的電動汽車革命早已展開,通過以新能源汽車替代汽/柴油車,中國正在大力實施一項將重塑全球汽車行業的計劃.![]() 年某企業計劃引進新能源汽車生產設備,通過市場分析,全年需投入固定成本
年某企業計劃引進新能源汽車生產設備,通過市場分析,全年需投入固定成本![]() 萬元,每生產
萬元,每生產![]() (百輛),需另投入成本
(百輛),需另投入成本![]() 萬元,且
萬元,且 .由市場調研知,每輛車售價
.由市場調研知,每輛車售價![]() 萬元,且全年內生產的車輛當年能全部銷售完.
萬元,且全年內生產的車輛當年能全部銷售完.
(1)求出2018年的利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (百輛)的函數關系式;(利潤=銷售額-成本)
(百輛)的函數關系式;(利潤=銷售額-成本)
(2)2018年產量為多少百輛時,企業所獲利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市場調查發現,某種產品在投放市場的30天中,其銷售價格P(元)和時間t(天)(t∈N)的關系如圖所示 
(1)寫出銷售價格P(元)和時間t(天)的函數解析式;
(2)若日銷售量Q(件)與時間t(天)的函數關系是Q=﹣t+40(0≤t≤30,t∈N),求該商品的日銷售金額y(元)與時間t(天)的函數解析式;
(3)問該產品投放市場第幾天時,日銷售金額最高?最高值為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知標有1~20號的小球20個,若我們的目的是估計總體號碼的平均值,即20個小球號碼的平均值.試驗者從中抽取4個小球,以這4個小球號碼的平均值估計總體號碼的平均值,按下面方法抽樣(按小號到大號排序):
(1)以編號2為起點,系統抽樣抽取4個球,則這4個球的編號的平均值為____.
(2)以編號3為起點,系統抽樣抽取4個球,則這4個球的編號的平均值為____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于利用斜二側法得到的直觀圖有下列結論:①三角形的直觀圖是三角形;②平行四邊形的直觀圖是平行四邊形;③正方形的直觀圖是正方形;④菱形的直觀圖是菱形,以上結論正確的是( )
A. ①② B. ① C. ③④ D. ①②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出以下命題:
(1)若![]() :
:![]() ;
;![]() :
:![]() ,則
,則![]() 為真,
為真,![]() 為假,
為假,![]() 為真
為真
(2)“![]() ”是“曲線
”是“曲線![]() 表示橢圓”的充要條件
表示橢圓”的充要條件
(3)命題“若![]() ,則
,則![]() ”的否命題為:“若
”的否命題為:“若![]() ,則
,則![]() ”
”
(4)如果將一組數據中的每一個數都加上同一個非零常數,那么這組數據的平均數和方差都改變;
則正確命題有( )個
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com