
【題目】已知雙曲線![]() 的中心在坐標原點,焦點在
的中心在坐標原點,焦點在![]() 軸上,離心率
軸上,離心率![]() ,虛軸長為2.
,虛軸長為2.
(1)求雙曲線![]() 的標準方程;
的標準方程;
(2)若直線![]() 與雙曲線
與雙曲線![]() 相交于
相交于![]() 兩點,(
兩點,( ![]() 均異于左、右頂點),且以
均異于左、右頂點),且以![]() 為直徑的圓過雙曲線
為直徑的圓過雙曲線![]() 的左頂點
的左頂點![]() ,求證:直線
,求證:直線![]() 過定點,并求出該定點的坐標.
過定點,并求出該定點的坐標.
【答案】(1) ![]() (2) 證明見解析,定點坐標為
(2) 證明見解析,定點坐標為![]()
【解析】試題分析:(1)求雙曲線標準方程,一般方法為待定系數法,即根據題意列出兩個獨立條件: ![]() ,解方程組得
,解方程組得![]() (2)以
(2)以![]() 為直徑的圓過雙曲線
為直徑的圓過雙曲線![]() 的左頂點
的左頂點![]() ,等價于
,等價于![]() ,根據向量數量積得
,根據向量數量積得![]() ,結合直線
,結合直線![]() 方程得
方程得![]() ,利用直線方程與雙曲線方程聯立方程組,消y得
,利用直線方程與雙曲線方程聯立方程組,消y得![]() ,再利用韋達定理代入等式整理得
,再利用韋達定理代入等式整理得![]() ,因此
,因此![]() 或
或![]() .逐一代入得當
.逐一代入得當![]() 時,
時, ![]() 的方程為
的方程為![]() ,直線過定點
,直線過定點![]() .
.
試題解析:(1)設雙曲線的標準方程為![]() , 由已知得
, 由已知得![]() 又
又![]() ,解得
,解得![]() ,所以雙曲線的標準方程為
,所以雙曲線的標準方程為![]() .
.
(2)設![]() ,聯立
,聯立 ,得
,得![]() ,有
,有 ,
,![]() ,以
,以![]() 為直徑的圓過雙曲線
為直徑的圓過雙曲線![]() 的左頂點
的左頂點![]() ,
,![]() ,即
,即 ,
,![]() ,解得
,解得![]() 或
或![]() .當
.當![]() 時,
時, ![]() 的方程為
的方程為![]() ,直線過定點
,直線過定點![]() ,與已知矛盾;當
,與已知矛盾;當![]() 時,
時, ![]() 的方程為
的方程為![]() ,直線過定點
,直線過定點![]() ,經檢驗符合已知條件, 所以直線
,經檢驗符合已知條件, 所以直線![]() 過定點,定點坐標為
過定點,定點坐標為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,設橢圓 ![]() (a>b>0)的左、右焦點分別為F1 , F2 , 點D在橢圓上.DF1⊥F1F2 ,
(a>b>0)的左、右焦點分別為F1 , F2 , 點D在橢圓上.DF1⊥F1F2 , ![]() =2
=2 ![]() ,△DF1F2的面積為
,△DF1F2的面積為 ![]() .
. 
(1)求橢圓的標準方程;
(2)設圓心在y軸上的圓與橢圓在x軸的上方有兩個交點,且圓在這兩個交點處的兩條切線相互垂直并分別過不同的焦點,求圓的半徑.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 被直線
被直線![]() ,
, ![]() 分成面積相等的四個部分,且截
分成面積相等的四個部分,且截![]() 軸所得線段的長為2.
軸所得線段的長為2.
(1)求![]() 的方程;
的方程;
(2)若存在過點![]() 的直線與
的直線與![]() 相交于
相交于![]() ,
, ![]() 兩點,且點
兩點,且點![]() 恰好是線段
恰好是線段![]() 的中點,求實數
的中點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一條光線從點(﹣2,﹣3)射出,經y軸反射后與圓(x+3)2+(y﹣2)2=1相切,則反射光線所在直線的斜率為( )
A.﹣![]() 或﹣
或﹣![]()
B.﹣![]() 或﹣
或﹣![]()
C.﹣![]() 或﹣
或﹣![]()
D.﹣![]() 或﹣
或﹣![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中不正確的是( )
A. 兩直線的斜率存在時,它們垂直的等價條件是其斜率之積為-1
B. 如果方程Ax+By+C=0表示的直線是y軸,那么系數A,B,C滿足A≠0,B=C=0
C. Ax+By+C=0和2Ax+2By+C+1=0表示兩條平行直線的等價條件是A2+B2≠0且C≠1
D. 與直線Ax+By+C=0垂直的直線系方程可設為Bx+Ay+m=0(m為參數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查某地區老年人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
性別 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估計該地區老年人中,需要志愿者提供幫助的老年人的比例;
(2)能否有99%的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關?
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,銳角![]() 和鈍角
和鈍角![]() 的終邊分別與單位圓交于
的終邊分別與單位圓交于![]() 兩點.
兩點.
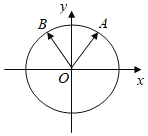
(Ⅰ)如果點![]() 縱坐標分別為
縱坐標分別為![]() ,求
,求![]() ;
;
(Ⅱ)若![]() 為
為![]() 軸上異于
軸上異于![]() 的點,且
的點,且![]() ,求點
,求點![]() 橫坐標的取值范圍.
橫坐標的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】求滿足下列條件的直線的方程:
(1)直線![]() 經過點
經過點![]() ,并且它的傾斜角等于直線
,并且它的傾斜角等于直線![]() 的傾斜角的2倍,求直線
的傾斜角的2倍,求直線![]() 的方程;
的方程;
(2)直線![]() 過點
過點![]() ,并且在
,并且在![]() 軸上的截距是
軸上的截距是![]() 軸上截距的
軸上截距的![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com