
���}Ŀ����֪����(sh��)![]()
��1����![]() ��
��![]() �ϵ���Сֵ��
�ϵ���Сֵ��
��2�����P(gu��n)��![]() �IJ���ʽ
�IJ���ʽ![]() ����ֻ������(g��)����(sh��)�⣬��(sh��)��(sh��)
����ֻ������(g��)����(sh��)�⣬��(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
���𰸡���1��ԔҊ��������2��![]() .
.
��������
��1���������(sh��)�Č�(d��o)��(sh��)��ͨ�^ӑՓm�ķ������������(sh��)�Ć��{(di��o)�^(q��)�g���Ķ��������(sh��)f��x�����]�^(q��)�g�ϵ���Сֵ���ɣ�
��2������(j��)f��x���Ć��{(di��o)�ԣ�ͨ�^ӑՓn�ķ�̖�����P(gu��n)��f��x���IJ���ʽ�Y(ji��)�ϲ���ʽ��Ă�(g��)��(sh��)�����n�ķ������ɣ�
�⣺��1��![]() ����
����![]() ����
����![]() ���f���^(q��)�g��
���f���^(q��)�g��![]() ����
����![]() ����
����![]() ���f�p�^(q��)�g��
���f�p�^(q��)�g��![]()
![]() ���t��(d��ng)
���t��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() �Ϟ�������(sh��)��
�Ϟ�������(sh��)��![]() ����Сֵ��
����Сֵ��![]() ��
��
��(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ��
��![]() �Ϟ�������(sh��)����
�Ϟ�������(sh��)����![]() �Ϟ�p����(sh��)����
�Ϟ�p����(sh��)����![]() ��
��
![]() ��
��![]() ��
��![]() ����Сֵ
����Сֵ![]() ����
����![]() ��
��![]() ����Сֵ��
����Сֵ��![]() ��
��
�C�ϣ���(d��ng)![]() �r(sh��)��
�r(sh��)��![]() ����Сֵ��
����Сֵ��![]() ����
����![]() ��
��![]() ����Сֵ��
����Сֵ��![]()
��2���ɣ�1��֪��![]() ���f���^(q��)�g��
���f���^(q��)�g��![]() ���f�p�^(q��)�g��
���f�p�^(q��)�g��![]() ������
������![]() �ϣ�
�ϣ�![]() ����
����![]() ���t
���t![]() ����
����![]() �r(sh��)���ɲ���ʽ
�r(sh��)���ɲ���ʽ![]() ��
��![]() ��
��![]() ����
����![]() �Ľ⼯��
�Ľ⼯��![]() ������(sh��)���Пo��(sh��)����(g��)�������}�⣻
������(sh��)���Пo��(sh��)����(g��)�������}�⣻
![]() �r(sh��)���ɲ���ʽ
�r(sh��)���ɲ���ʽ![]() ����
����![]() ���⼯��
���⼯��![]() ������(sh��)���Пo��(sh��)����(g��)�������}�⣻
������(sh��)���Пo��(sh��)����(g��)�������}�⣻
![]() �r(sh��)�ɲ���ʽ
�r(sh��)�ɲ���ʽ![]() ����
����![]() ��
��![]() ��
��![]() �Ľ⼯��
�Ľ⼯��![]() �o����(sh��)�⣬������ʽ
�o����(sh��)�⣬������ʽ![]() ����ֻ������(g��)����(sh��)�⣬
����ֻ������(g��)����(sh��)�⣬![]() ��
��![]() �f������
�f������![]() �f�p����
�f�p����![]() ����
����![]() �����ԣ�����(g��)������(sh��)1��2��3����
�����ԣ�����(g��)������(sh��)1��2��3����![]() ���C�ϣ���(sh��)��(sh��)
���C�ϣ���(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������![]() .
.


 53�S�Üyϵ�д�
53�S�Üyϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���O(sh��)![]() ��
��![]() ��
��![]() ��
��![]() ��ƽ��ֱ������(bi��o)ϵ�ЃɃɲ�ͬ���c(di��n)����
��ƽ��ֱ������(bi��o)ϵ�ЃɃɲ�ͬ���c(di��n)����![]() ��
��![]() ����
����![]() ���t�Q�c(di��n)
���t�Q�c(di��n)![]() ��
��![]() �{(di��o)�ͷָ��c(di��n)
�{(di��o)�ͷָ��c(di��n)![]() ��
��![]() ����֪ƽ�����c(di��n)
����֪ƽ�����c(di��n)![]() ��
��![]() �{(di��o)�ͷָ��c(di��n)
�{(di��o)�ͷָ��c(di��n)![]() ��
��![]() .�t�����f�����_���ǣ�����
.�t�����f�����_���ǣ�����
A. ![]() �����Ǿ���
�����Ǿ���![]() �����c(di��n)
�����c(di��n)
B. ![]() �����Ǿ���
�����Ǿ���![]() �����c(di��n)
�����c(di��n)
C. �c(di��n)![]() ��
��![]() ����ͬ�r(sh��)�ھ���
����ͬ�r(sh��)�ھ���![]() ��
��
D. �c(di��n)![]() ��
��![]() ������ͬ�r(sh��)�ھ���
������ͬ�r(sh��)�ھ���![]() �����L����
�����L����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���ں����M(j��n)�й��̽��O(sh��)�r(sh��)��һ����Ҫ�ڹ���ij̎�O(sh��)�þ���ˮ�F(xi��n)��һ�������I(y��)����ӛ���c(di��n)![]() ����һ��(g��)�ض��r(sh��)��(n��i)�����c(di��n)
����һ��(g��)�ض��r(sh��)��(n��i)�����c(di��n)![]() �����ĵ�1�����ԃ�(n��i)�����O(sh��)�龯��ˮ���c(di��n)
�����ĵ�1�����ԃ�(n��i)�����O(sh��)�龯��ˮ���c(di��n)![]() ����
����![]() ����̎��һ��(g��)���_(d��)�^�yվ
����̎��һ��(g��)���_(d��)�^�yվ![]() ��ij�r(sh��)�̜y��һ�҄���ֱ�����Ĵ�ֻλ���c(di��n)
��ij�r(sh��)�̜y��һ�҄���ֱ�����Ĵ�ֻλ���c(di��n)![]() ��ƫ�|
��ƫ�|![]() ���c�c(di��n)
���c�c(di��n)![]() ���10������
���10�����λ��![]() ����(j��ng)�^12����֜y��ԓ�������c(di��n)
����(j��ng)�^12����֜y��ԓ�������c(di��n)![]() ��ƫ�|
��ƫ�|![]() ���c�c(di��n)
���c�c(di��n)![]() ���
���![]() ������
������![]() .
.
��1����ԓ��������ٶȣ���λ������/С�r(sh��)����
��2����ԓ������׃���з����^�m(x��)���.ԇ�Д����Ƿ��(hu��)�M(j��n)�뾯��ˮ���c(di��n)![]() �c���ľ��xС��1���T���M(j��n)�뾯��ˮ�����f������.
�c���ľ��xС��1���T���M(j��n)�뾯��ˮ�����f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���Ŵ�����ʮ���һ��(g��)������ʮ��ɺ�ʮ����֧������ʮ��݆һ�飬�ܶ���(f��)ʼ�����Ӟ��֧֮һ�����?y��n)��һ��(g��)ǰһλ�ǹﺥ����һλ���ҳ�Փ�����У����֮���֮ľ����֧֮�ӌ��֮ˮ����ˮ��ľ������ʮ���cʮ��֧�����Ƀ����䣬�ļ��ӵ��ﺥ������ʮ��(g��)�M�ϣ��Q��ʮ����.
���}
��1��2020���Ǽ����꣬���ٶ���������Ǽ����ꣿ
��2����һ��(g��)�Ѻ��굽��һ��(g��)�����꣬�����Ƕ��٣�
��3��Ӌ(j��)��i��![]() ,
,![]() ��
��![]() ������һֱӋ(j��)����ȥ�����(hu��)�õ�ʲô�Y(ji��)Փ��
������һֱӋ(j��)����ȥ�����(hu��)�õ�ʲô�Y(ji��)Փ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() ��ǰn�(xi��ng)�͞�
��ǰn�(xi��ng)�͞�![]() ���ҝM��
���ҝM��![]() ����(sh��)��
����(sh��)��![]() ��
��![]() ��������������(sh��)
��������������(sh��)![]() ��
��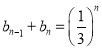 .
.
��1����(sh��)��![]() ��ͨ�(xi��ng)��ʽ��
��ͨ�(xi��ng)��ʽ��
��2���Ƿ���ڌ�(sh��)��(sh��)![]() ��ʹ�Ô�(sh��)��
��ʹ�Ô�(sh��)��![]() �ǵȱȔ�(sh��)�У������ڣ�Ո�����(sh��)��(sh��)
�ǵȱȔ�(sh��)�У������ڣ�Ո�����(sh��)��(sh��)![]() ������q��ֵ���������ڣ�Ո�f�����ɣ�
������q��ֵ���������ڣ�Ո�f�����ɣ�
��3����(sh��)��![]() ǰn�(xi��ng)��
ǰn�(xi��ng)��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij�۞���ƽ��ʾ��D��D��ʾ��![]() ��
��![]() ��
��![]() �քe�Ǻ�����
�քe�Ǻ�����![]() ��
��![]() �ϵ�����(g��)���(zh��n)��
�ϵ�����(g��)���(zh��n)��![]() λ��
λ��![]() �����Ϸ���
�����Ϸ���![]() ̎��
̎��![]() λ��
λ��![]() �ı�ƫ�|
�ı�ƫ�|![]() ����
����![]() ̎.�S����(j��ng)��(j��)�İl(f��)չ���龏�⼯�(zh��n)
̎.�S����(j��ng)��(j��)�İl(f��)չ���龏�⼯�(zh��n)![]() �Ľ�ͨ�������M�ں�����
�Ľ�ͨ�������M�ں�����![]() ��
��![]() �Ϸքe���a�^
�Ϸքe���a�^![]() ��
��![]() ���_��ˮ�Ϻ��������y�r(sh��)�l(f��)�F(xi��n)����
���_��ˮ�Ϻ��������y�r(sh��)�l(f��)�F(xi��n)����![]() ��A�ģ�
��A�ģ�![]() ��돽�����΅^(q��)��?y��n)�\ˮ�^(q��)�����m�˴�ֻ����.
��돽�����΅^(q��)��?y��n)�\ˮ�^(q��)�����m�˴�ֻ����.
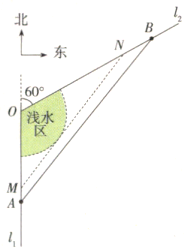
��1���ܷ�������(zh��n)![]() ��
��![]() �g��ֱ�����x��
�g��ֱ�����x��
��2������(j��)���yҪ��Ҫʹ![]() ��
��![]() ֮�g��ֱ��������̣�ֱ��
֮�g��ֱ��������̣�ֱ��![]() �c�A
�c�A![]() ��(y��ng)�M��ʲô�P(gu��n)ϵ��
��(y��ng)�M��ʲô�P(gu��n)ϵ��
��3����(y��ng)���Ӵ_���a�^![]() ��
��![]() ��λ�ã�����ʹ��
��λ�ã�����ʹ��![]() ��
��![]() ֮�g��ֱ��������̣�
֮�g��ֱ��������̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����1��2����������n������![]() �Ă�(g��)��(sh��)��ʹ��
�Ă�(g��)��(sh��)��ʹ��![]() ��������(sh��)k=1��2����������n������
��������(sh��)k=1��2����������n������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�AE�� ![]() ���������⌍(sh��)��(sh��)k������ֱ�����E�AE�صõ����L�cl��y��kx��1���E�AE�صõ����L��������ȵ���(����)
���������⌍(sh��)��(sh��)k������ֱ�����E�AE�صõ����L�cl��y��kx��1���E�AE�صõ����L��������ȵ���(����)
A. kx��y��k��0 B. kx��y��1��0
C. kx��y��k��0 D. kx��y��2��0
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����o����֮�¡��IJ���,��Ҍ��F������Σ�����˸��M(j��n)һ�����J(r��n)�R(sh��),�����F�������о�Ҳ�u�u���S����,ij�о��C(j��)��(g��u)������(ji��)ȼ�ş���������씵(sh��)x�c�F���씵(sh��)y�M(j��n)�нy(t��ng)Ӌ(j��)����,�ó��±픵(sh��)��(j��).
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)Ո����(j��)�ϱ��ṩ�Ĕ�(sh��)��(j��),����С���˷����y�P(gu��n)��x�ľ��Իؚw����![]() ��
��
(2)ԇ����(j��)(1)����ľ��Իؚw����,�A(y��)�yȼ�ş���������씵(sh��)��9���F���씵(sh��).
(���P(gu��n)��ʽ�� )
)
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com