
【題目】某港灣的平面示意圖如圖所示,![]() 、
、![]() 、
、![]() 分別是海岸線
分別是海岸線![]() 、
、![]() 上的三個集鎮,
上的三個集鎮,![]() 位于
位于![]() 的正南方向
的正南方向![]() 處,
處,![]() 位于
位于![]() 的北偏東
的北偏東![]() 方向
方向![]() 處.隨著經濟的發展,為緩解集鎮
處.隨著經濟的發展,為緩解集鎮![]() 的交通壓力,擬在海岸線
的交通壓力,擬在海岸線![]() 、
、![]() 上分別修建碼頭
上分別修建碼頭![]() 、
、![]() ,開辟水上航線,勘測時發現:以
,開辟水上航線,勘測時發現:以![]() 為圓心,
為圓心,![]() 為半徑的扇形區域為淺水區,不適宜船只航行.
為半徑的扇形區域為淺水區,不適宜船只航行.
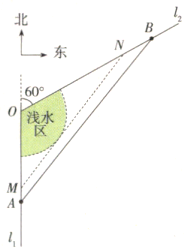
(1)能否求出集鎮![]() 、
、![]() 間的直線距離?
間的直線距離?
(2)根據勘測要求,要使![]() 、
、![]() 之間的直線航線最短,直線
之間的直線航線最短,直線![]() 與圓
與圓![]() 應滿足什么關系?
應滿足什么關系?
(3)應怎樣確定碼頭![]() 、
、![]() 的位置,才能使得
的位置,才能使得![]() 、
、![]() 之間的直線航線最短?
之間的直線航線最短?
【答案】(1)![]() ;(2)直線
;(2)直線![]() 與圓
與圓![]() 應該相切;(3)碼頭
應該相切;(3)碼頭![]() 、
、![]() 與集鎮
與集鎮![]() 的距離均為
的距離均為![]() 時,
時,![]() 、
、![]() 之間的直線航線最短.
之間的直線航線最短.
【解析】
(1)在![]() 中,利用余弦定理可求出
中,利用余弦定理可求出![]() 的長度;
的長度;
(2)要使![]() 、
、![]() 之間的直線航線最短,又使得航線
之間的直線航線最短,又使得航線![]() 不能經過淺水區,進而可得知直線
不能經過淺水區,進而可得知直線![]() 與圓
與圓![]() 的位置關系;
的位置關系;
(3)設直線![]() 與圓
與圓![]() 相切于點
相切于點![]() ,連接
,連接![]() ,設
,設![]() ,
,![]() ,
,![]() ,根據
,根據![]() 的面積得到等式
的面積得到等式![]() ,然后利用余弦定理結合基本不等式求出
,然后利用余弦定理結合基本不等式求出![]() 的最小值,利用等號成立的條件求出
的最小值,利用等號成立的條件求出![]() 、
、![]() ,進而可得出結論.
,進而可得出結論.
(1)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
根據余弦定理得![]()
![]() ,所以
,所以![]() ,故集鎮
,故集鎮![]() 、
、![]() 間的直線距離為
間的直線距離為![]() ;
;
(2)要使![]() 、
、![]() 之間的直線航線最短,又使得航線
之間的直線航線最短,又使得航線![]() 不能經過淺水區,則直線
不能經過淺水區,則直線![]() 與圓
與圓![]() 應該相切;
應該相切;
(3)設直線![]() 與圓
與圓![]() 相切于點
相切于點![]() ,連接
,連接![]() ,則
,則![]() .
.
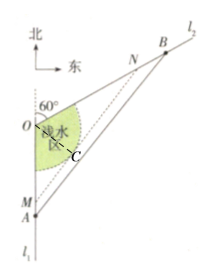
設![]() ,
,![]() ,
,![]() ,
,
在![]() 中,由
中,由![]() ,
,
得![]() ,即
,即![]() ,
,
由余弦定理,得![]() ,
,
所以![]() ,解得
,解得![]() ,
,
當且僅當![]() 時,
時,![]() 取得最小值
取得最小值![]() ,
,
所以碼頭![]() 、
、![]() 與集鎮
與集鎮![]() 的距離均為
的距離均為![]() 時,
時,![]() 、
、![]() 之間的直線航線最短,最短距離為
之間的直線航線最短,最短距離為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左焦點為
的左焦點為![]() ,過點
,過點![]() 的直線交橢圓于
的直線交橢圓于![]() ,
,![]() 兩點,
兩點,![]() 的最大值是
的最大值是![]() ,
,![]() 的最小值是
的最小值是![]() ,且滿足
,且滿足![]() .
.
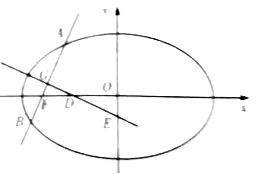
(1)求橢圓的離心率;
(2)設線段![]() 的中點為
的中點為![]() ,線段
,線段![]() 的垂直平分線與
的垂直平分線與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點,
兩點,![]() 是坐標原點,記
是坐標原點,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,一輛汽車從![]() 市出發沿海岸一條筆直公路以每小時
市出發沿海岸一條筆直公路以每小時![]() 的速度向東均速行駛,汽車開動時,在
的速度向東均速行駛,汽車開動時,在![]() 市南偏東方向距
市南偏東方向距![]() 市
市![]() 且與海岸距離為
且與海岸距離為![]() 的海上
的海上![]() 處有一快艇與汽車同時出發,要把一份稿件交給這汽車的司機.
處有一快艇與汽車同時出發,要把一份稿件交給這汽車的司機.
(1)快艇至少以多大的速度行駛才能把稿件送到司機手中?
(2)在(1)的條件下,求快艇以最小速度行駛時的行駛方向與![]() 所成的角.
所成的角.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,已知直線l過點![]() .
.
(1)若直線l的縱截距和橫截距相等,求直線l的方程;
(2)若直線l與兩坐標軸圍成的三角形的面積為![]() ,求直線l的方程.
,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,點B是
的直徑,點B是![]() 上與A,C不重合的動點,
上與A,C不重合的動點,![]() 平面
平面![]() .
.

(1)當點B在什么位置時,平面![]() 平面
平面![]() ,并證明之;
,并證明之;
(2)請判斷,當點B在![]() 上運動時,會不會使得
上運動時,會不會使得![]() ,若存在這樣的點B,請確定點B的位置,若不存在,請說明理由.
,若存在這樣的點B,請確定點B的位置,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】①若直線![]() 與曲線
與曲線![]() 有且只有一個公共點,則直線
有且只有一個公共點,則直線![]() 一定是曲線
一定是曲線![]() 的切線;
的切線;
②若直線![]() 與曲線
與曲線![]() 相切于點
相切于點![]() ,且直線
,且直線![]() 與曲線
與曲線![]() 除點
除點![]() 外再沒有其他的公共點,則在點
外再沒有其他的公共點,則在點![]() 附近,直線
附近,直線![]() 不可能穿過曲線
不可能穿過曲線![]() ;
;
③若![]() 不存在,則曲線
不存在,則曲線![]() 在點
在點![]() 處就沒有切線;
處就沒有切線;
④若曲線![]() 在點
在點![]() 處有切線,則
處有切線,則![]() 必存在.
必存在.
則以上論斷正確的個數是( )
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市政府為了鼓勵居民節約用水,計劃調整居民生活用水收費方案,擬確定一個合理的月用水量標準![]() (噸)、一位居民的月用水量不超過
(噸)、一位居民的月用水量不超過![]() 的部分按平價收費,超出
的部分按平價收費,超出![]() 的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
的部分按議價收費.為了了解居民用水情況,通過抽樣,獲得了某年100位居民每人的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.

(Ⅰ)求直方圖中a的值;
(Ⅱ)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,并說明理由;
(Ⅲ)若該市政府希望使85%的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值,并說明理由.
的值,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com