
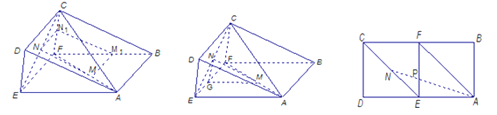
【題目】如圖,已知三棱柱BCF﹣ADE的側面CFED與ABFE都是邊長為1的正方形,M、N兩點分別在AF和CE上,且AM=EN.
(1)求證:平面ABCD⊥平面ADE;
(2)求證:MN∥平面BCF;
(3)若點N為EC的中點,點P為EF上的動點,試求PA+PN的最小值.
【答案】解:(1)∵四邊形CFED與ABFE都是正方形
∴EF⊥DE,EF⊥AE,又DE∩EA=E,∴EF⊥平面ADE,
又∵EF∥AB,∴AB⊥平面ADE
∵AB平面ABCD,∴平面ABCD⊥平面ADE
(2)證法一:過點M作MM1⊥BF交BF于M1 ,
過點N作NN1⊥CF交BF于N1 , 連結M1N1 ,
∵MM1∥AB,NN1∥EF∴MM1∥NN1
又∵![]() ,
,
∴MM1=NN1
∴四邊形MNN1M1為平行四邊形,
∴MN∥N1M1 , 又MN面BCF,N1M1面BCF,∴MN∥面BCF.
[法二:過點M作MG⊥EF交EF于G,連結NG,則![]() ,∴NG∥CF
,∴NG∥CF
又NG面BCF,CF面BCF,∴NG∥面BCF,
同理可證得MG∥面BCF,又MG∩NG=G,∴平面MNG∥平面BCF
∵MN平面MNG,∴MN∥面BCF.
(3)如圖將平面EFCD繞EF旋轉到與ABFE在同一平面內,則當點
A、P、N在同一直線上時,PA+PN最小,
在△AEN中,∵![]()
由余弦定理得AN2=AE2+EN2﹣2AEENcos135°,
∴AN=![]() ,
,
即![]() .
.
【解析】(1)四邊形CFED與ABFE都是正方形,利用線面垂直可得EF⊥平面ADE,再根據EF∥AB,得出AB⊥平面ADE,最后利用面面垂直的判定得出結論;
(2)證法一:過點M作MM1⊥BF交BF于M1 , 過點N作NN1⊥CF交BF于N1 , 連結M1N1 , 先證得四邊形MNN1M1為平行四邊形,得MN∥N1M1 , 再根據線面平行的判定得到MN∥面BCF.
法二:過點M作MG⊥EF交EF于G,連結NG,得出平面MNG∥平面BCF,最后利用面面平行的性質得出MN∥面BCF;
(3)將平面EFCD繞EF旋轉到與ABFE在同一平面內,則當點A、P、N在同一直線上時,PA+PN最小.通過解△AEN,利用余弦定理求出AN即可。
【考點精析】本題主要考查了直線與平面平行的判定和平面與平面垂直的判定的相關知識點,需要掌握平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行;一個平面過另一個平面的垂線,則這兩個平面垂直才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】為了研究“晚上喝綠茶與失眠”有無關系,調查了100名人士,得到下面的列聯表:
失眠 | 不失眠 | 合計 | |
晚上喝綠茶 | 16 | 40 | 56 |
晚上不喝綠茶 | 5 | 39 | 44 |
合計 | 21 | 79 | 100 |
由已知數據可以求得:![]() ,則根據下面臨界值表:
,則根據下面臨界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
可以做出的結論是( )
A. 在犯錯誤的概率不超過0.01的前提下認為“晚上喝綠茶與失眠有關”
B. 在犯錯誤的概率不超過0.01的前提下認為“晚上喝綠茶與失眠無關”
C. 在犯錯誤的概率不超過0.05的前提下認為“晚上喝綠茶與失眠有關”
D. 在犯錯誤的概率不超過0.05的前提下認為“晚上喝綠茶與失眠無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex+![]() .
.
(I)當a=![]() 時,求函數f(x)在x=0處的切線方程;
時,求函數f(x)在x=0處的切線方程;
(II)函數f(x)是否存在零點?若存在,求出零點的個數;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某植物園準備建一個五邊形區域的盆栽館,三角形ABE為盆裁展示區,沿AB、AE修建觀賞長廊,四邊形BCDE是盆栽養護區,若BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=![]() 米。
米。
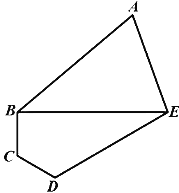
(1)求兩區域邊界BE的長度;
(2)若區域ABE為銳角三角形,求觀賞長廊總長度AB+AE的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠為檢驗車間一生產線是否工作正常,現從生產線中隨機抽取一批零件樣本,測量尺寸(單位: mm )繪成頻率分布直方圖如圖所示:
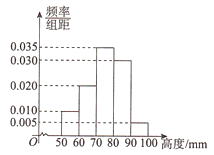
(Ⅰ)求該批零件樣本尺寸的平均數 x 和樣本方差 ![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(Ⅱ)若該批零件尺寸![]() 服從正態分布
服從正態分布 ![]() ,其中
,其中 ![]() 近似為樣本平均數
近似為樣本平均數 ![]() 近似為樣本方差
近似為樣本方差 ![]() ,利用該正態分布求
,利用該正態分布求 ![]() ;
;
(Ⅲ)若從生產線中任取一零件,測量尺寸為30mm,根據 ![]() 原則判斷該生產線是否正常?
原則判斷該生產線是否正常?
附: ![]() ;若
;若![]() ,則
,則 ![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用a代表紅球,b代表藍球,c代表黑球,由加法原理及乘法原理,從1個紅球和1個藍球中取出若干個球的所有取法可由(1+a)(1+b)的展開式1+a+b+ab表示出來,如:“1”表示一個球都不取、“a”表示取出一個紅球,而“ab”則表示把紅球和藍球都取出來.以此類推,下列各式中,其展開式可用來表示從5個無區別的紅球、5個無區別的藍球、5個有區別的黑球中取出若干個球,且所有的藍球都取出或都不取出的所有取法的是( )
A.(1+a+a2+a3+a4+a5)(1+b5)(1+c)5
B.(1+a5)(1+b+b2+b3+b4+b5)(1+c)5
C.(1+a)5(1+b+b2+b3+b4+b5)(1+c5)
D.(1+a5)(1+b)5(1+c+c2+c3+c4+c5)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com