
已知函數f(x)=x2-4,設曲線y=f(x)在點(xn,f(xn))
處的切線與x軸的交點為(xn+1,0)(n∈N+),其中x1為正實數.
(1)用xn表示xn+1;
(2)求證:對一切正整數n,xn+1≤xn的充要條件是x1≥2;
(3)若x1=4,記an=lg  ,證明數列{an}成等比數列,并求數列{xn}的通項公式.
,證明數列{an}成等比數列,并求數列{xn}的通項公式.
科目:高中數學 來源: 題型:解答題
某校要建一個面積為450平方米的矩形球場,要求球場的一面利用舊墻,其他各面用鋼筋網圍成,且在矩形一邊的鋼筋網的正中間要留一個3米的進出口(如圖).設矩形的長為 米,鋼筋網的總長度為
米,鋼筋網的總長度為 米.
米.
(1)列出 與
與 的函數關系式,并寫出其定義域;
的函數關系式,并寫出其定義域;
(2)問矩形的長與寬各為多少米時,所用的鋼筋網的總長度最小?
(3)若由于地形限制,該球場的長和寬都不能超過25米,問矩形的長與寬各為多少米時,所用的鋼筋網的總長度最小?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某地方政府在某地建一座橋,兩端的橋墩相距m米,此工程只需建兩端橋墩之間的橋面和橋墩(包括兩端的橋墩).經預測,一個橋墩的費用為256萬元,相鄰兩個橋墩之間的距離均為x,且相鄰兩個橋墩之間的橋面工程費用為(1+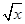 )x萬元,假設所有橋墩都視為點且不考慮其他因素,記工程總費用為y萬元.
)x萬元,假設所有橋墩都視為點且不考慮其他因素,記工程總費用為y萬元.
(1)試寫出y關于x的函數關系式;
(2)當m=1280米時,需要新建多少個橋墩才能使y最小?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=x2+mx+n的圖象過點(1,3),且f(-1+x)=f(-1-x)對任意實數都成立,函數y=g(x)與y=f(x)的圖象關于原點對稱.
(1)求f(x)與g(x)的解析式;
(2)若F(x)=g(x)-λf(x)在(-1,1]上是增函數,求實數λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
首屆世界低碳經濟大會在南昌召開,本屆大會以“節能減排,綠色生態”為主題.某單位在國家科研部門的支持下,進行技術攻關,采用了新工藝,把二氧化碳轉化為一種可利用的化工產品.已知該單位每月的處理量最少為400噸,最多為600噸,月處理成本y(元)與月處理量x(噸)之間的函數關系可近似地表示為y=x2-200x+80 000,且每處理一噸二氧化碳得到可利用的化工產品價值為100元.
(1)該單位每月處理量為多少噸時,才能使每噸的平均處理成本最低?
(2)該單位每月能否獲利?如果獲利,求出最大利潤;如果不獲利,則國家至少需要補貼多少元才能使該單位不虧損?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設函數f(x)=ax2+bx+b-1(a≠0).
(1)當a=1,b=-2時,求函數f(x)的零點;
(2)若對任意b∈R,函數f(x)恒有兩個不同零點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知函數f(x)=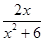 .
.
(1)若f(x)>k的解集為{x|x<-3,或x>-2},求k的值;
(2)對任意x>0,f(x)≤t恒成立,求t的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com