試題分析:(1)
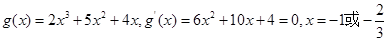
, 2分
由單調(diào)性即得
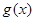
極大值為
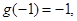
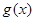
極小值為
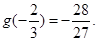
6分
(2)
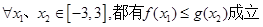
,即
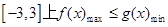
,
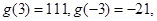

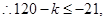
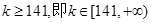
12分
點評:求函數(shù)的最值極值一般首先通過導(dǎo)數(shù)求得極值點,第二問中的不等式恒成立轉(zhuǎn)化為求
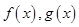
的最值并比較大小
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
設(shè)函數(shù)
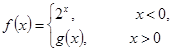
若
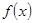
是奇函數(shù),則
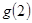
的值是( )
A.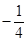 | B.-4 | C.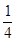 | D.4 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
設(shè)函數(shù)
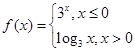
,則
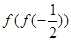
=
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)
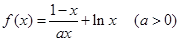
(I)當(dāng)
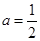
時,求

在[1,
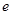
]上的取值范圍。
(II)若
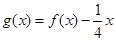
在[1,
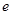
]上為增函數(shù),求a的取值范圍。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)
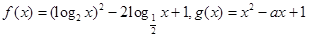
(1)求函數(shù)
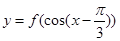
的定義域;
(2)若存在
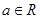
,對任意
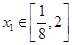
,總存在唯一
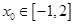
,使得
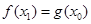
成立.求實數(shù)
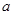
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
對于函數(shù)
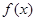
,在使
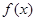
≥M恒成立的所有常數(shù)M中,我們把M中的最大值稱為函數(shù)
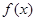
的“下確界”,則函數(shù)
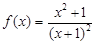
的下確界為_______________.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)
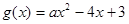
的遞增區(qū)間是
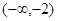
① 求
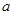
的值。
② 設(shè)
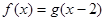
,求
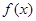
在區(qū)間
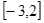
上的最大值和最小值。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知
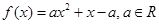
.
(1)若
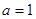
,解不等式
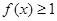
;
(2)若不等式
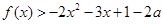
對一切實數(shù)
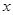
恒成立,求實數(shù)
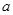
的取值范圍;
(3)若
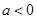
,解不等式
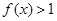
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
已知函數(shù)

(1)解關(guān)于
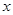
的不等式
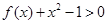
(2)若
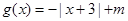
,
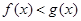
的解集非空,求實數(shù)m的取值范圍
查看答案和解析>>

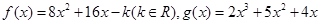 .
. 極值;
極值;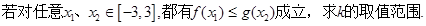
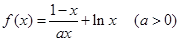
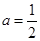 時,求
時,求 在[1,
在[1,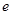 ]上的取值范圍。
]上的取值范圍。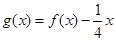 在[1,
在[1,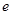 ]上為增函數(shù),求a的取值范圍。
]上為增函數(shù),求a的取值范圍。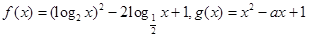
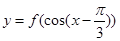 的定義域;
的定義域;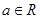 ,對任意
,對任意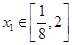 ,總存在唯一
,總存在唯一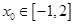 ,使得
,使得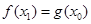 成立.求實數(shù)
成立.求實數(shù)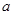 的取值范圍.
的取值范圍.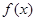 ,在使
,在使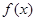 ≥M恒成立的所有常數(shù)M中,我們把M中的最大值稱為函數(shù)
≥M恒成立的所有常數(shù)M中,我們把M中的最大值稱為函數(shù)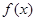 的“下確界”,則函數(shù)
的“下確界”,則函數(shù)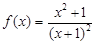 的下確界為_______________.
的下確界為_______________.