
【題目】已知![]() 為常數(shù),
為常數(shù), ![]() ,函數(shù)
,函數(shù)![]() ,
, ![]() (其中
(其中![]() 是自然對數(shù)的底數(shù)).
是自然對數(shù)的底數(shù)).
(1)過坐標(biāo)原點(diǎn)![]() 作曲線
作曲線![]() 的切線,設(shè)切點(diǎn)為
的切線,設(shè)切點(diǎn)為![]() ,求證:
,求證: ![]() ;
;
(2)令![]() ,若函數(shù)
,若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)函數(shù),求
上是單調(diào)函數(shù),求![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】試題分析:(1)先對函數(shù)求導(dǎo), ![]() ,可得切線的斜率
,可得切線的斜率![]() ,即
,即![]() ,由
,由![]() 是方程的解,且
是方程的解,且![]() 在
在![]() 上是增函數(shù),可證;(2)由
上是增函數(shù),可證;(2)由![]() ,
, 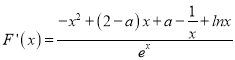 ,先研究函數(shù)
,先研究函數(shù)![]() ,則
,則![]() ,由
,由![]() 在
在![]() 上是減函數(shù),可得
上是減函數(shù),可得![]() ,通過研究
,通過研究![]() 的正負(fù)可判斷
的正負(fù)可判斷![]() 的單調(diào)性,進(jìn)而可得函數(shù)
的單調(diào)性,進(jìn)而可得函數(shù)![]() 的單調(diào)性,可求出參數(shù)范圍.
的單調(diào)性,可求出參數(shù)范圍.
試題解析:(1)![]() (
(![]() ),
),
所以切線的斜率![]() ,
,
整理得![]() ,顯然,
,顯然, ![]() 是這個(gè)方程的解,
是這個(gè)方程的解,
又因?yàn)?/span>![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
所以方程![]() 有唯一實(shí)數(shù)解,
有唯一實(shí)數(shù)解,
故![]() .
.
(2)![]() ,
, 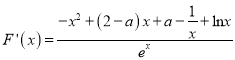 ,
,
設(shè)![]() ,則
,則![]() ,
,
易知![]() 在
在![]() 上是減函數(shù),從而
上是減函數(shù),從而![]() .
.
①當(dāng)![]() ,即
,即![]() 時(shí),
時(shí), ![]() ,
, ![]() 在區(qū)間
在區(qū)間![]() 上是增函數(shù),
上是增函數(shù),
∵![]() ,∴
,∴![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),所以
上是減函數(shù),所以![]() 滿足題意.
滿足題意.
②當(dāng)![]() ,即
,即![]() 時(shí),設(shè)函數(shù)
時(shí),設(shè)函數(shù)![]() 的唯一零點(diǎn)為
的唯一零點(diǎn)為![]() ,
,
則![]() 在
在![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,
又∵![]() ,∴
,∴![]() ,
,
又∵![]() ,
,
∴![]() 在
在![]() 內(nèi)有唯一一個(gè)零點(diǎn)
內(nèi)有唯一一個(gè)零點(diǎn)![]() ,
,
當(dāng)![]() 時(shí),
時(shí), ![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí), ![]() .
.
從而![]() 在
在![]() 遞減,在
遞減,在![]() 遞增,與在區(qū)間
遞增,與在區(qū)間![]() 上是單調(diào)函數(shù)矛盾.
上是單調(diào)函數(shù)矛盾.
∴![]() 不合題意.綜上①②得,
不合題意.綜上①②得, ![]() .
.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 為等差數(shù)列
為等差數(shù)列![]() 的前n項(xiàng)和,
的前n項(xiàng)和,![]() 是正項(xiàng)等比數(shù)列,且
是正項(xiàng)等比數(shù)列,且![]() ,
,![]() .在①
.在①![]() ,②
,②![]() ,③
,③![]() 這三個(gè)條件中任選一個(gè),回答下列為題:
這三個(gè)條件中任選一個(gè),回答下列為題:
(1)求數(shù)列![]() 和
和![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)如果![]() (m,
(m,![]() ),寫出m,n的關(guān)系式
),寫出m,n的關(guān)系式![]() ,并求
,并求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() :
:![]() ,點(diǎn)
,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 是圓
是圓![]() 上任意一點(diǎn),線段
上任意一點(diǎn),線段![]() 的垂直平分線交線段
的垂直平分線交線段![]() 于點(diǎn)
于點(diǎn)![]() .
.
(1)求點(diǎn)![]() 的軌跡方程.
的軌跡方程.
(2)設(shè)點(diǎn)![]() ,
,![]() 是
是![]() 的軌跡上異于頂點(diǎn)的任意兩點(diǎn),以
的軌跡上異于頂點(diǎn)的任意兩點(diǎn),以![]() 為直徑的圓過點(diǎn)
為直徑的圓過點(diǎn)![]() .求證直線
.求證直線![]() 過定點(diǎn),并求出該定點(diǎn)的坐標(biāo).
過定點(diǎn),并求出該定點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】環(huán)保部門要對所有的新車模型進(jìn)行廣泛測試,以確定它的行車?yán)锍痰牡燃墸冶硎菍?100 輛新車模型在一個(gè)耗油單位內(nèi)行車?yán)锍蹋▎挝唬汗铮┑臏y試結(jié)果.
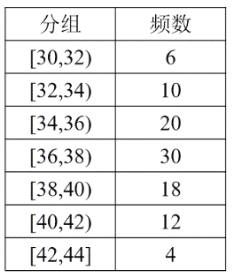
(Ⅰ)做出上述測試結(jié)果的頻率分布直方圖,并指出其中位數(shù)落在哪一組;
(Ⅱ)用分層抽樣的方法從行車?yán)锍淘趨^(qū)間[38,40)與[40,42)的新車模型中任取5輛,并從這5輛中隨機(jī)抽取2輛,求其中恰有一個(gè)新車模型行車?yán)锍淘赱40,42)內(nèi)的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=|x-m|-|2x+2m|(m>0).
(Ⅰ)當(dāng)m=1時(shí),求不等式f(x)≥1的解集;
(Ⅱ)若x∈R,t∈R,使得f(x)+|t-1|<|t+1|,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() (
(![]() ,
,![]() ).
).
(1)當(dāng)![]() 時(shí),
時(shí),![]() 在
在![]() 上是單調(diào)遞增函數(shù),求
上是單調(diào)遞增函數(shù),求![]() 的取值范圍;
的取值范圍;
(2)當(dāng)![]() 時(shí),討論函數(shù)
時(shí),討論函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)對于任意給定的正實(shí)數(shù)![]() ,證明:存在實(shí)數(shù)
,證明:存在實(shí)數(shù)![]() ,使得
,使得![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】影響消費(fèi)水平的原因很多,其中重要的一項(xiàng)是工資收入.研究這兩個(gè)變量的關(guān)系的一個(gè)方法是通過隨機(jī)抽樣的方法,在一定范圍內(nèi)收集被調(diào)查者的工資收入和他們的消費(fèi)狀況.下面的數(shù)據(jù)是某機(jī)構(gòu)收集的某一年內(nèi)上海、江蘇、浙江、安徽、福建五個(gè)地區(qū)的職工平均工資與城鎮(zhèn)居民消費(fèi)水平(單位:萬元).
地區(qū) | 上海 | 江蘇 | 浙江 | 安徽 | 福建 |
職工平均工資 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城鎮(zhèn)居民消費(fèi)水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江蘇、浙江、安徽三個(gè)地區(qū)的職工平均工資和他們的消費(fèi)水平,求出線性回歸方程![]() ,其中
,其中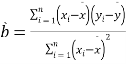
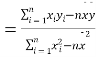 ,
,![]() ;
;
(2)若由線性回歸方程得到的估計(jì)數(shù)據(jù)與所選出的檢驗(yàn)數(shù)據(jù)的誤差均不超過1萬,則認(rèn)為得到的線性回歸方程是可靠的,試問所得的線性回歸方程是否可靠?(![]() 的結(jié)果保留兩位小數(shù))
的結(jié)果保留兩位小數(shù))
(參考數(shù)據(jù):![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直三棱柱ABC-A1B1C1中,AA1![]() AB
AB![]() AC
AC![]() 2,AB⊥AC,M是棱BC的中點(diǎn)點(diǎn)P在線段A1B上.
2,AB⊥AC,M是棱BC的中點(diǎn)點(diǎn)P在線段A1B上.
(1)若P是線段A1B的中點(diǎn),求直線MP與直線AC所成角的大小;
(2)若![]() 是
是![]() 的中點(diǎn),直線
的中點(diǎn),直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求線段BP的長度.
,求線段BP的長度.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com