
已知函數(shù)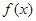 滿足對一切
滿足對一切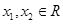 都有
都有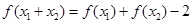 ,且
,且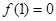 ,當
,當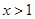 時有
時有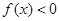 .
.
(1)求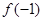 的值;
的值;
(2)判斷并證明函數(shù)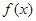 在
在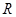 上的單調(diào)性;
上的單調(diào)性;
(3)解不等式: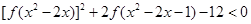 .
.
(1) 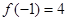
(2)利用函數(shù)的定義法來證明函數(shù)單調(diào)性,注意設變量的任意性,以及作差法,變形定號,下結(jié)論的步驟。
(3)
【解析】
試題分析:解:⑴令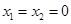 ,得
,得 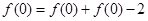 ,
, 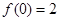
再令 ,得
,得 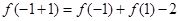 ,
,
即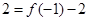 ,從而
,從而 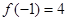 . 2分
. 2分
⑵任取
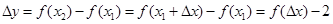 4分
4分
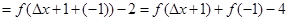
 .
.
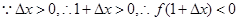 ,即
,即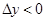 .
.
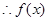 在
在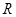 上是減函數(shù).
6分
上是減函數(shù).
6分
⑶由條件知,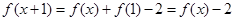 ,
,
設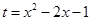 ,則
,則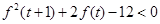 ,即
,即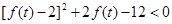 ,
,
整理,得  , 8分
, 8分
而 ,
,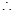 不等式即為
不等式即為 ,
,
又因為 在
在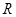 上是減函數(shù),
上是減函數(shù),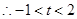 ,即
,即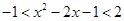 ,
10分
,
10分
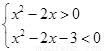 ,從而所求不等式的解集為
,從而所求不等式的解集為 .
12分
.
12分
考點:抽象函數(shù)的性質(zhì)
點評:解決的關鍵是利用賦值法思想求值,同時借助于函數(shù)單調(diào)性定義證明單調(diào)性,從而解不等式。屬于基礎題。


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:高中數(shù)學 來源:2015屆遼寧省五校協(xié)作體高一上學期聯(lián)合競賽數(shù)學試卷(解析版) 題型:解答題
(本小題滿分12分)
已知函數(shù)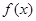 滿足對一切
滿足對一切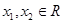 都有
都有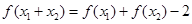 ,且
,且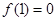 ,
,
當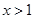 時有
時有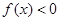 .
.
(1)求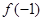 的值;
的值;
(2)判斷并證明函數(shù)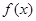 在
在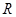 上的單調(diào)性;
上的單調(diào)性;
(3)解不等式: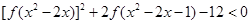 .
.
查看答案和解析>>
科目:高中數(shù)學 來源:2014屆遼寧省大連市高一期末數(shù)學試卷 題型:解答題
)已知函數(shù) 滿足對一切
滿足對一切 都有
都有 ,且
,且 ,當
,當 時有
時有 .
.
(1)求 的值;
的值;
(2)判斷并證明函數(shù) 在
在 上的單調(diào)性;
上的單調(diào)性;
(3)解不等式:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
(本題滿分12分)已知函數(shù)![]() 滿足對一切
滿足對一切![]() 都有
都有![]() ,且
,且![]() ,當
,當![]() 時有
時有![]() .
.
⑴求![]() 的值;
的值;
⑵判斷并證明函數(shù)![]() 在
在![]() 上的單調(diào)性;
上的單調(diào)性;
⑶解不等式:![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com