
【題目】已知函數f(x)= ![]() . (I)求函數f(x)的單調區間;
. (I)求函數f(x)的單調區間;
(II)若不等式f(x)> ![]() 恒成立,求整數k的最大值;
恒成立,求整數k的最大值;
(III)求證:(1+1×2)(1+2×3)…(1+n(n×1))>e2n﹣3(n∈N*).
【答案】解:(Ⅰ)f(x)的定義域是(0,1)∪(1,+∞), f′(x)=﹣  ,
,
令φ(x)= ![]() +lnx,則φ′(x)=
+lnx,則φ′(x)= ![]() ,
,
x∈(0,1)時,φ′(x)<0,φ(x)遞減,
∴φ(x)>φ(1)=1>0,
∴f′(x)<0,f(x)遞減,
x∈(1,+∞)時,φ′(x)>0,φ(x)遞增,
∴φ(x)>φ(1)=1>0,∴f′(x)<0,f(x)遞減,
綜上,f(x)在(0,1),(1,+∞)遞減;
(Ⅱ)f(x)> ![]() (x>1)恒成立,
(x>1)恒成立,
令h(x)= ![]() >k恒成立,
>k恒成立,
即h(x)的最小值大于k,
h′(x)= ![]() ,(x>1),
,(x>1),
令g(x)=x﹣2﹣lnx(x>1),則g′(x)= ![]() >0,
>0,
故g(x)在(1,+∞)遞增,
又g(3)=1﹣ln3<0,g(4)=2﹣2ln2>0,
g(x)=0存在唯一的實數根a,且滿足a∈(3,4),a﹣2﹣lna=0,
故x>a時,g(x)>0,h′(x)>0,h(x)遞增,
1<x<a時,g(x)<0,h′(x)<0,h(x)遞減,
故h(x)min=h(a)= ![]() =
= ![]() =a∈(3,4),
=a∈(3,4),
故正整數k的最大值是3;
(Ⅲ)法一:由(Ⅱ)知, ![]() >
> ![]() ,(x>1)恒成立,
,(x>1)恒成立,
即lnx>2﹣ ![]() ,故ln(x+1)>2﹣
,故ln(x+1)>2﹣ ![]() >2﹣
>2﹣ ![]() ,
,
令x=n(n+1),(n∈N*),得ln[1+n(n+1)]>2﹣ ![]() ,
,
∴ln(1+1×2)+ln(1+2×3)+…+ln[1+n(n+1)]
>(2﹣ ![]() )+(2﹣
)+(2﹣ ![]() )+…+[2﹣
)+…+[2﹣ ![]() ]
]
=2n﹣3[ ![]() +
+ ![]() +…+
+…+ ![]() ]
]
=2n﹣3(1﹣ ![]() )
)
=2n﹣3+ ![]() >2n﹣3,
>2n﹣3,
故(1+1×2)(1+2×3)…(1+n(n×1))>e2n﹣3(n∈N*).
法二:要證(1+1×2)(1+2×3)(1+3×4)…(1+n(n+1))>e2n﹣3 ,
只需證ln[(1+1×2)(1+2×3)(1+3×4)…(1+n(n+1))]>2n﹣3,
即ln(1+12)+ln(1+23)+…+ln(1+n(n+1))>2n﹣3.
可以下面利用數學歸納法證明:
①當n=1時 左邊=ln3>0,右邊=﹣1,不等式顯然成立;
②當n=2時 左邊=ln3+ln7=ln21 右邊=1 顯然不等式成立;
③假設n=k( k≥2)時成立,即ln1+12)+ln(1+23)+…+ln(1+k(k+1)>2k﹣3,
那么n=k+1時,
ln(1+12)+ln(1+23)+…+ln(1+(k+1)(k+2))
=ln(1+12)+ln(1+23)+…+ln(1+k(k+1))+ln(1+(k+1)(k+2))
>2k﹣3+ln(1+(k+1)(k+2))
∵當k≥2時 ln(1+(k+1)(k+2))>2.
∴ln(1+12)+ln(1+23)+…+ln(1+(k+1)(k+2))
>2k﹣3+2=2k﹣1=2(k+1)﹣3,
∴當n=k+1時不等式成立.
綜上所述ln(1+12)+ln(1+23)+…+ln(1+n(n+1))>2n﹣3成立.
則(1+1×2)(1+2×3)(1+3×4)…(1+n(n+1))>e2n﹣3 .
【解析】(Ⅰ)對函數f(x)求導數,可判f′(x)<0,進而可得單調性;(Ⅱ)問題轉化為h(x)k恒成立,通過構造函數可得h(x)min∈(3,4),進而可得k值;(Ⅲ)法一:可得ln(x+1)>2﹣ ![]() ,令x=n(n+1)(n∈N*),一系列式子相加,由裂項相消法可得ln(1+1×2)+ln(1+2×3)+…+ln[1+n(n+1)]>2n﹣3,進而可得答案;法二:利用數學歸納法證明即可.
,令x=n(n+1)(n∈N*),一系列式子相加,由裂項相消法可得ln(1+1×2)+ln(1+2×3)+…+ln[1+n(n+1)]>2n﹣3,進而可得答案;法二:利用數學歸納法證明即可.
【考點精析】根據題目的已知條件,利用利用導數研究函數的單調性和函數的最大(小)值與導數的相關知識可以得到問題的答案,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣ax+ ![]() (a∈R).
(a∈R).
(1)當a=﹣ ![]() 時,求函數f(x)的單調區間和極值.
時,求函數f(x)的單調區間和極值.
(2)若g(x)=f(x)+a(x﹣1)有兩個零點x1 , x2 , 且x1<x2 , 求證:x1+x2>1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中學校共有學生1800名,各年級男女學生人數如表.已知在全校學生中隨機抽取1名,抽到高二女生的概率是0.16.
高一年級 | 高二年級 | 高三年級 | |
女生 | 324 | x | 280 |
男生 | 316 | 312 | y |
現用分層抽樣的方法,在全校抽取45名學生,則應在高三抽取的學生人數為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的通項公式為an=2n﹣1(n∈N*),且a2 , a5分別是等比數列{bn}的第二項和第三項,設數列{cn}滿足cn= ![]() ,{cn}的前n項和為Sn
,{cn}的前n項和為Sn
(1)求數列{bn}的通項公式;
(2)是否存在m∈N* , 使得Sm=2017,并說明理由
(3)求Sn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)是定義在(﹣∞,0)上的可導函數,其導函數為f′(x),且有xf′(x)>x2+3f(x),則不等式8f(x+2014)+(x+2014)3f(﹣2)>0的解集為( )
A.(﹣∞,﹣2016)
B.(﹣2018,﹣2016)
C.(﹣2018,0)
D.(﹣∞,﹣2018)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣x2與g(x)=(x﹣2)2﹣ ![]() ﹣m的圖象上存在關于(1,0)對稱的點,則實數m的取值范圍是( )
﹣m的圖象上存在關于(1,0)對稱的點,則實數m的取值范圍是( )
A.(﹣∞,1﹣ln2)
B.(﹣∞,1﹣ln2]
C.(1﹣ln2,+∞)
D.[1﹣ln2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下四個命題: ①已知隨機變量X~N(0,σ2),若P(|X|<2)=a,則P(X>2)的值為 ![]() ;
;
②設a、b∈R,則“log2a>log2b”是“2a﹣b>1”的充分不必要條件;
③函數f(x)= ![]() ﹣(
﹣( ![]() )x的零點個數為1;
)x的零點個數為1;
④命題p:n∈N,3n≥n2+1,則¬p為n∈N,3n≤n2+1.
其中真命題的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直三棱柱ABC﹣A1B1C1中,AC⊥BC,AC=BC= ![]() AA1=1,D是棱AA1上的點,DC1⊥BD
AA1=1,D是棱AA1上的點,DC1⊥BD
(Ⅰ)求證:D為AA1中點;
(Ⅱ)求直線BC1與平面BDC所成角正弦值大小;
(Ⅲ)在△ABC邊界及內部是否存在點M,使得B1M⊥面BDC,存在,說明M位置,不存在,說明理由.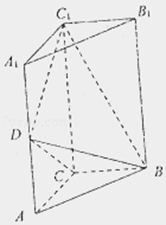
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com