
【題目】已知函數![]()
(1)當![]() 時,求函數
時,求函數![]() 的單調遞增區間;
的單調遞增區間;
(2)在區間![]() 內至少存在一個實數
內至少存在一個實數![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)單調遞增區間是![]() 和
和![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)先確定函數,然后對函數進行求導,利用導數的正負建立不等式,求得函數的單調性與單調區間;(2)先對函數進行求導,然后通過分類討論,確定函數的單調性,求得函數的最小值,利用最小值小于0,建立不等式,求解不等式,得到實數的取值范圍.
試題解析:(1)當![]() 時,
時, ![]() ,由
,由![]() ,得
,得![]() 或
或![]() ,
,
所以函數![]() 在
在![]() 與
與![]() 上為增函數,
上為增函數,
即函數![]() 的單調遞增區間是
的單調遞增區間是![]() 和
和![]() .
.
(2) ![]() ,
,
當![]() ,即
,即![]() 時,
時, ![]() 在[1,2]恒成立,
在[1,2]恒成立,
![]() 在[1,2]上為增函數,故
在[1,2]上為增函數,故![]() ,
,
所以![]() ,這與
,這與![]() 矛盾.
矛盾.
當![]() ,即
,即![]() 時,若
時,若![]() ,則
,則![]() ;
;
若![]() ,則
,則![]() 所以當
所以當![]() 時,
時, ![]() 取得最小值,
取得最小值,
因此![]() ,即
,即![]() ,可得
,可得![]() ,
,
這與![]() 矛盾.
矛盾.
當![]() ,即
,即![]() 時,
時, ![]() 在[1,2]恒成立,
在[1,2]恒成立, ![]() 在[1,2]上為減函數,
在[1,2]上為減函數,
所以![]() ,
,
所以![]() ,解得
,解得![]() ,滿足
,滿足![]() .
.
綜上所述,實數![]() 的取值范圍為
的取值范圍為![]()


 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案科目:高中數學 來源: 題型:
【題目】平面α外有兩條直線m和n,如果m和n在平面α內的投影分別是m1和n1,給出下列四個命題:①m1⊥n1m⊥n;②m⊥nm1⊥n1;③m1與n1相交m與n相交或重合;④m1與n1平行m與n平行或重合.其中不正確的命題個數是( )
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AC是圓O的直徑,點B在圓O上,∠BAC=30°,BM⊥AC于點M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.

(1)證明:EM⊥BF;
(2)求平面BEF與平面ABC所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于集合![]() ,定義了一種運算“
,定義了一種運算“![]() ”,使得集合
”,使得集合![]() 中的元素間滿足條件:如果存在元素
中的元素間滿足條件:如果存在元素![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,則稱元素
,則稱元素![]() 是集合
是集合![]() 對運算“
對運算“![]() ”的單位元素.例如:
”的單位元素.例如: ![]() ,運算“
,運算“![]() ”為普通乘法;存在
”為普通乘法;存在![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,所以元素
,所以元素![]() 是集合
是集合![]() 對普通乘法的單位元素.
對普通乘法的單位元素.
下面給出三個集合及相應的運算“![]() ”:
”:
①![]() ,運算“
,運算“![]() ”為普通減法;
”為普通減法;
②![]() {
{![]() 表示
表示![]() 階矩陣,
階矩陣, ![]() },運算“
},運算“![]() ”為矩陣加法;
”為矩陣加法;
③![]() (其中
(其中![]() 是任意非空集合),運算“
是任意非空集合),運算“![]() ”為求兩個集合的交集.
”為求兩個集合的交集.
其中對運算“![]() ”有單位元素的集合序號為( )
”有單位元素的集合序號為( )
A. ①②; B. ①③; C. ①②③; D. ②③.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 為圓柱
為圓柱![]() 的母線,
的母線, ![]() 是底面圓
是底面圓![]() 的直徑,
的直徑, ![]() 是
是![]() 的中點.
的中點.
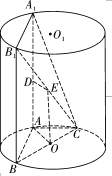
(Ⅰ)問: ![]() 上是否存在點
上是否存在點![]() 使得
使得![]() 平面
平面![]() ?請說明理由;
?請說明理由;
(Ⅱ)在(Ⅰ)的條件下,若![]() 平面
平面![]() ,假設這個圓柱是一個大容器,有條體積可以忽略不計的小魚能在容器的任意地方游弋,如果小魚游到四棱錐
,假設這個圓柱是一個大容器,有條體積可以忽略不計的小魚能在容器的任意地方游弋,如果小魚游到四棱錐![]() 外會有被捕的危險,求小魚被捕的概率.
外會有被捕的危險,求小魚被捕的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,
, ![]() (
(![]() ).
).
(1)當![]() 時,若函數
時,若函數![]() 與
與![]() 的圖象在
的圖象在![]() 處有相同的切線,求
處有相同的切線,求![]() 的值;
的值;
(2)當![]() 時,若對任意
時,若對任意![]() 和任意
和任意![]() ,總存在不相等的正實數
,總存在不相等的正實數![]() ,使得
,使得![]() ,求
,求![]() 的最小值;
的最小值;
(3)當![]() 時,設函數
時,設函數![]() 與
與![]() 的圖象交于
的圖象交于![]()
![]() 兩點.求證:
兩點.求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐PABCD中,AD∥BC,平面PAC⊥平面ABCD,AB=AD=DC=1,
∠ABC=∠DCB=60,E是PC上一點.
(Ⅰ)證明:平面EAB⊥平面PAC;
(Ⅱ)若△PAC是正三角形,且E是PC中點,求三棱錐AEBC的體積.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解用戶對其產品的滿意度,從A、B兩地區分別隨機調查了20個用戶,得到用戶對產品的滿意度評分如下:
A地區: | 62 | 73 | 81 | 92 | 95 | 85 | 74 | 64 | 53 | 76 |
78 | 86 | 95 | 66 | 97 | 78 | 88 | 82 | 76 | 89 | |
B地區: | 73 | 83 | 62 | 51 | 91 | 46 | 53 | 73 | 64 | 82 |
93 | 48 | 95 | 81 | 74 | 56 | 54 | 76 | 65 | 79 |
(Ⅰ)根據兩組數據完成兩地區用戶滿意度評分的莖葉圖,并通過莖葉圖比較兩地區滿意度的平均值及分散程度(不要求算出具體值,給出結論即可):

(Ⅱ)根據用戶滿意度評分,將用戶的滿意度從低到高分為三個等級:
滿意度評分 | 低于70分 | 70分到89分 | 不低于90分 |
滿意度等級 | 不滿意 | 滿意 | 非常滿意 |
記事件C:“A地區用戶的滿意度等級高于B地區用戶的滿意度等級”,假設兩地區用戶的評價結果相互獨立,根據所給數據,以事件發生的頻率作為相應事件發生的概率,求C的概率。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com