
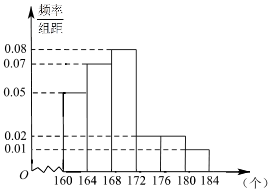
 《漢字聽寫大會》不斷創收視新高,為了避免“書寫危機”弘揚傳統文化,某市對全市10萬名市民進行了漢字聽寫測試,調查數據顯示市民的成績服從正態分布N(168,16).現從某社區居民中隨機抽取50名市民進行聽寫測試,發現被測試市民正確書寫漢字的個數全部在160到184之間,將測試結果按如下方式分成六組:第一組[160,164),第二組[164,168),…,第六組[180,184),如圖是按上述分組方法得到的頻率分布直方圖.
《漢字聽寫大會》不斷創收視新高,為了避免“書寫危機”弘揚傳統文化,某市對全市10萬名市民進行了漢字聽寫測試,調查數據顯示市民的成績服從正態分布N(168,16).現從某社區居民中隨機抽取50名市民進行聽寫測試,發現被測試市民正確書寫漢字的個數全部在160到184之間,將測試結果按如下方式分成六組:第一組[160,164),第二組[164,168),…,第六組[180,184),如圖是按上述分組方法得到的頻率分布直方圖.分析 (1)利用組中值代替本組數據計算平均值,和168比較得出結論;求出后3組的面積之和,再乘上總人數得出成績在172個以上(含172個)的人數;
(2)利用正態分布得出全市前130名的成績,得出50名社區居民中符合條件的人數,使用超幾何分布的概率公式得出分布列.
解答 解:(1)該社區50名市民的平均成績為162×0.05×4+166×0.07×4+170×0.08×4+174×0.02×4+178×0.02×4+182×0.01×4=168.72,
∴該社區被測試的50名市民的成績略高于全市市民的平均成績.
50名市民中成績在172個以上(含172個)的人數為50×(0.02+0.02+0.01)×4=10.
(2)∵P(168-3×4≤ξ<168+3×4)=0.9974,∴P(ξ≥180)=$\frac{1}{2}$(1-0.9974)=0.0013,
∵0.0013×100 000=130.
∴全市前130名的成績在180個以上(含180個),
這50人中成績在180 個以上(含180個)的有2人.
∴隨機變量ξ的可能取值為0,1,2,
∴P(ξ=0)=$\frac{{C}_{8}^{2}}{{C}_{10}^{2}}$=$\frac{28}{45}$,P(ξ=1)=$\frac{{C}_{8}^{1}{•C}_{2}^{1}}{{C}_{10}^{2}}$=$\frac{16}{45}$,P(ξ=2)=$\frac{{C}_{2}^{2}}{{C}_{10}^{2}}$=$\frac{1}{45}$,
∴E(ξ)=0×$\frac{28}{45}$+1×$\frac{16}{45}$+2×$\frac{1}{45}$=$\frac{2}{5}$.
點評 本題考查了頻率分布直方圖,正態分布與超幾何分布,屬于中檔題.


科目:高中數學 來源: 題型:選擇題

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | i | D. | -i |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {1} | B. | {(1,3)} | C. | {(1,2)} | D. | {2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com