
【題目】某鋼鐵加工廠新生產一批鋼管,為了了解這批產品的質量狀況,檢驗員隨機抽取了![]() 件鋼管作為樣本進行檢測,將它們的內徑尺寸作為質量指標值,由檢測結果得如下頻率分布表和頻率分布直方圖:
件鋼管作為樣本進行檢測,將它們的內徑尺寸作為質量指標值,由檢測結果得如下頻率分布表和頻率分布直方圖:
分組 | 頻數 | 頻率 |
|
|
|
| ||
|
| |
| ||
| ||
|
|
|
|
|
|
合計 |
|
|

(1)求![]() ,
,![]() ;
;
(2)根據質量標準規定:鋼管內徑尺寸大于等于![]() 或小于
或小于![]() 為不合格,鋼管內徑尺寸在
為不合格,鋼管內徑尺寸在![]() 或
或![]() 為合格,鋼管內徑尺寸在
為合格,鋼管內徑尺寸在![]() 為優等.鋼管的檢測費用為
為優等.鋼管的檢測費用為![]() 元/根,把樣本的頻率分布作為這批鋼管的概率分布.
元/根,把樣本的頻率分布作為這批鋼管的概率分布.
(i)若從這批鋼管中隨機抽取![]() 根,求內徑尺寸為優等鋼管根數
根,求內徑尺寸為優等鋼管根數![]() 的分布列和數學期望;
的分布列和數學期望;
(ii)已知這批鋼管共有![]() 根,若有兩種銷售方案:
根,若有兩種銷售方案:
第一種方案:不再對該批剩余鋼管進行檢測,扣除![]() 根樣品中的不合格鋼管后,其余所有鋼管均以
根樣品中的不合格鋼管后,其余所有鋼管均以![]() 元/根售出;
元/根售出;
第二種方案:對該批鋼管進行一一檢測,不合格鋼管不銷售,并且每根不合格鋼管損失![]() 元,合格等級的鋼管
元,合格等級的鋼管![]() 元/根,優等鋼管
元/根,優等鋼管![]() 元/根.
元/根.
請你為該企業選擇最好的銷售方案,并說明理由.
【答案】(1)![]() ,
,![]() (2)(i)分布列見解析,期望為0.9(ii)當
(2)(i)分布列見解析,期望為0.9(ii)當![]() 時,按第一種方案,
時,按第一種方案,
![]() 時,第一、二種方案均可,
時,第一、二種方案均可, ![]() 時,按第二種方案.
時,按第二種方案.
【解析】
(1)結合列聯表和頻率直方圖運用,計算b、a值,即可。(2)(i)分別計算X=0,1,2,3對應的概率,列出分布列,計算期望,即可。(ii)分別計算每種方案對應的利潤,然后相減,計算出m的范圍,即可。
(1)由題意知:![]() ,
,
所以![]()
![]() ,
,
所以![]() .
.
(2)(i)由(1)知,鋼管內徑尺寸為優等的概率為![]() ,
,![]() 所有可能的取值為
所有可能的取值為![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
故![]() 的分布列為
的分布列為
|
|
|
|
|
|
|
|
|
|
![]()
(ii)按第一種方案:![]()
![]() ,
,
按第二種方案:![]()
![]() ,
,
![]()
![]() ,
,
若![]() 時,
時,![]() ,則按第一種方案,
,則按第一種方案,
若![]() 時,
時,![]() ,則第一、第二方案均可,
,則第一、第二方案均可,
若![]() 時,
時,![]() ,則按第二種方案,
,則按第二種方案,
故當![]() 時,按第一種方案,
時,按第一種方案,
![]() 時,第一、二種方案均可,
時,第一、二種方案均可,
![]() 時,按第二種方案.
時,按第二種方案.


科目:高中數學 來源: 題型:
【題目】[2019·濰坊期末]某鋼鐵加工廠新生產一批鋼管,為了了解這批產品的質量狀況,檢驗員隨機抽取了100件鋼管作為樣本進行檢測,將它們的內徑尺寸作為質量指標值,由檢測結果得如下頻率分布表和頻率分布直方圖:
分組 | 頻數 | 頻率 |
25.05~25.15 | 2 | 0.02 |
25.15~25.25 | ||
25.25~25.35 | 18 | |
25.35~25.45 | ||
25.45~25.55 | ||
25.55~25.65 | 10 | 0.1 |
25.65~25.75 | 3 | 0.03 |
合計 | 100 | 1 |

(1)求![]() ,
,![]() ;
;
(2)根據質量標準規定:鋼管內徑尺寸大于等于25.75或小于25.15為不合格,鋼管尺寸在![]() 或
或![]() 為合格等級,鋼管尺寸在
為合格等級,鋼管尺寸在![]() 為優秀等級,鋼管的檢測費用為0.5元/根.
為優秀等級,鋼管的檢測費用為0.5元/根.
(i)若從![]() 和
和![]() 的5件樣品中隨機抽取2根,求至少有一根鋼管為合格的概率;
的5件樣品中隨機抽取2根,求至少有一根鋼管為合格的概率;
(ii)若這批鋼管共有2000根,把樣本的頻率作為這批鋼管的頻率,有兩種銷售方案:
①對該批剩余鋼管不再進行檢測,所有鋼管均以45元/根售出;
②對該批剩余鋼管一一進行檢測,不合格產品不銷售,合格等級的鋼管50元/根,優等鋼管60元/根.
請你為該企業選擇最好的銷售方案,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】由國家公安部提出,國家質量監督檢驗檢疫總局發布的《車輛駕駛人員血液、呼氣酒精含量閥值與檢驗標準(GB/T19522-2010)》于2011年7月1日正式實施.車輛駕駛人員酒飲后或者醉酒后駕車血液中的酒精含量閥值見表.經過反復試驗,一般情況下,某人喝一瓶啤酒后酒精在人體血液中的變化規律的“散點圖”見圖,且圖表示的函數模型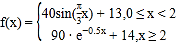 ,則該人喝一瓶啤酒后至少經過多長時間才可以駕車(時間以整小時計算)?(參考數據:
,則該人喝一瓶啤酒后至少經過多長時間才可以駕車(時間以整小時計算)?(參考數據:![]() ,
,![]() )
)
駕駛行為類型 | 閥值 |
飲酒后駕車 |
|
醉酒后駕車 |
|
車輛駕車人員血液酒精含量閥值

喝1瓶啤酒的情況
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】建設生態文明,是關系人民福祉,關乎民族未來的長遠大計.某市通宵營業的大型商場,為響應節能減排的號召,在氣溫超過![]() 時,才開放中央空調降溫,否則關閉中央空調.如圖是該市夏季一天的氣溫(單位:
時,才開放中央空調降溫,否則關閉中央空調.如圖是該市夏季一天的氣溫(單位:![]() )隨時間(
)隨時間(![]() ,單位:小時)的大致變化曲線,若該曲線近似的滿足函數
,單位:小時)的大致變化曲線,若該曲線近似的滿足函數![]() 關系.
關系.
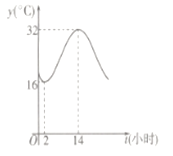
(1)求函數![]() 的表達式;
的表達式;
(2)請根據(1)的結論,判斷該商場的中央空調應在本天內何時開啟?何時關閉?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:對棱相等的四面體為等腰四面體.
(1)若等腰四面體的每條棱長都是![]() ,求該等腰四面體的體積;
,求該等腰四面體的體積;
(2)求證:等腰四面體每個面的三角形均為銳角三角形:
(3)設等腰四面體![]() 的三個側面與底面所成的角分別為
的三個側面與底面所成的角分別為![]() ,請判斷
,請判斷![]() 是否為定值?如果是定值,請求出該定值;如果不是定值,請說明理由.
是否為定值?如果是定值,請求出該定值;如果不是定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有4名學生參加演講比賽,有![]() 兩個題目可供選擇,組委會決定讓選手通過擲一枚質地均勻的骰子選擇演講的題目,規則如下:選手擲出能被3整除的數則選擇
兩個題目可供選擇,組委會決定讓選手通過擲一枚質地均勻的骰子選擇演講的題目,規則如下:選手擲出能被3整除的數則選擇![]() 題目,擲出其他的數則選擇
題目,擲出其他的數則選擇![]() 題目.
題目.
(1)求這4個人中恰好有1個人選擇![]() 題目的概率;
題目的概率;
(2)用![]() 分別表示這4個人中選擇
分別表示這4個人中選擇![]() 題目的人數,記
題目的人數,記![]() ,求隨機變量
,求隨機變量![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com