
【題目】若函數f(x)=ax2-(3a-1)x+a2在[1,+∞)上是增函數,求實數a的取值范圍.
【答案】0≤a≤1.
【解析】試題分析:先討論參數a是否為0,若a=0,代入可得一次函數是增函數,成立;若a≠0,則二次函數開口向上,且x=1在對稱軸的右側,列出不等式解出a的范圍即可.
試題解析:
①a=0時,f(x)=x在[1,+∞)上是增函數.
②a≠0時,∵f(x)在[1,+∞)上是增函數.
∴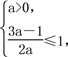 解得0<a≤1.
解得0<a≤1.
綜上0≤a≤1.
點睛:本題考查一次函數和二次函數的單調性,屬于基礎題.根據函數解析式的形式,先要對最高次項的系數進行討論,當a=0時,函數為一次函數,將a=0代入可知一次項系數為正,故為增函數;當a≠0時,函數為二次函數,若要使函數在[1,+∞)上是增函數,則需要開口向上,且[1,+∞)為增區間的子集,比較對稱軸和1的大小關系列出不等式求解即可.


科目:高中數學 來源: 題型:
【題目】袋子中有四個小球,分別寫有“幸”“福”“快”“樂”四個字,有放回地從中任取一個小球,取到“快”就停止,用隨機模擬的方法估計直到第二次停止的概率:先由計算器產生1到4之間取整數值的隨機數,且用1,2,3,4表示取出小球上分別寫有“幸”“福”“快”“樂”四個字,以每兩個隨機數為一組,代表兩次的結果,經隨機模擬產生了20組隨機數:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
據此估計,直到第二次就停止的概率為( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點
的右焦點![]() ,橢圓
,橢圓![]() 的左,右頂點分別為
的左,右頂點分別為![]() .過點
.過點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,且
兩點,且![]() 的面積是
的面積是![]() 的面積的3倍.
的面積的3倍.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() 與
與![]() 軸垂直,
軸垂直,![]() 是橢圓
是橢圓![]() 上位于直線
上位于直線![]() 兩側的動點,且滿足
兩側的動點,且滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值,請說明理由.
的斜率是否為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市公租房的房源位于![]() 四個片區,設每位申請人只申請其中一個片區的房源,且申請其中任一個片區的房源是等可能的,在該市的甲、乙、丙三位申請人中:
四個片區,設每位申請人只申請其中一個片區的房源,且申請其中任一個片區的房源是等可能的,在該市的甲、乙、丙三位申請人中:
(1)求恰有1人申請![]() 片區房源的概率;
片區房源的概率;
(2)用![]() 表示選擇
表示選擇![]() 片區的人數,求
片區的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人玩擲骰子游戲,甲擲出的點數記為![]() ,乙擲出的點數記為
,乙擲出的點數記為![]() ,
,
若關于![]() 的一元二次方程
的一元二次方程![]() 有兩個不相等的實數根時甲勝;方程有
有兩個不相等的實數根時甲勝;方程有
兩個相等的實數根時為“和”;方程沒有實數根時乙勝.
(1)列出甲、乙兩人“和”的各種情形;
(2)求甲勝的概率.
必要時可使用此表格

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017屆河南省鄭州市第一中學高三上學期第一次質量檢測數學(文)】已知函數![]() .
.
(1)證明:![]() ;
;
(2)若對任意![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com